Isometries: Translation, Rotation, Reflection
Pre-requisites
You should know trigonometry and basic highschool algebra.
Review of the Rectangular Coordinate System
We use a pair of numbers {x,y} to identify a point in the plane. The first number x in {x,y} indicates the horizontal position of the point, and the second number indicates height of the point in the plane. For example, {3,4} would be a point positioned at 3 units to the right and 4 units above. {-2,-5} would be a point 2 units to the left, and 5 units down.
The point {0,0} is very useful, we call it the Origin, and we denote the point O.
Direction of a Point
A point in the plane has a direction with respect to the origin. For example, going from {0,0} to {1,0} is heading east. Going from {0,0} to {0,-1} is heading west. Going from {0,0} to {1,1} is north east.
A point's direction is specified precisely by the angle it makes with the positive x-axis. For example, the point {1,0} would have angle 0, and the point {1,1} would have angle π/4, and point {-1,0} would have angle π.
Length of a Point
We can define a length for a point as the distance from the origin to the point.
From trigonometry, we know that the length of a point with coordinate {x,y} can be expressed as Sqrt[x^2+y^2].
Translation of a Point
Sometimes we like to move a whole image in the plane to a new location.
By Translation, we mean moving a point to a new position. For example, if we have a point A:={3,4}, and we want to move it 2 units to the right and 6 units up, then the new point would have a coordinates of {3+2, 4+6}.
We think of translation as addition of two points. For example, if A:={3,4} and B:={2,6}, then A+B=={5,10}.
Dilation of a Point
Sometimes we like to magnify or shrink a image in the plane. We call these processes together as dilation.
In the concept of magnification or shrink, there must be a center. So, when we do dilation, we choose the origin as the center of dilation. A dilation can be specified by a scaling factor.
If we have a point A:={a,b}, and we want a new point B, such that B is in the same direction of vector A, but is longer by a factor of r, then the new point has the coordinate {r*a,r*b}.
Proof: This is so, because we know the length of {a,b} is Sqrt[a^2+b^2]. Now, the length and direction of the new point {r*a,r*b} is Sqrt[(r*a)^2+(r*b)^2], which simplifies to Sqrt[r^2*(a^2+b^2)] and r*Sqrt[a^2+b^2], which is just r times the length of A.
The direction of {a,b} is the direction of the new point {r*a,r*b} is ArcTan[(r*b)/(r*a)], which simplifies to ArcTan[b/a]. So we know that the direction is unchanged.
Suppose a point A has α angle with the positive x-axis, and the distance from A to origin is r. From trigonometry, we know that its coordinate would be {r*Cos[α],r*Sin[α]}.
Rotation
Sometimes we like to rotate a whole image of the plane around the origin. Given a point {a,b}, what's the coordinate of the point rotated by α around the origin?
Let's say point A has angle α. From trigonometry, we can write point A as {r*Cos[α],r*Sin[α]} where r is the length of A. The point A rotated around origin by β can be written as {r*Cos[α+β],r*Sin[α+β]}.
From trig identities, we can rewrite {r*Cos[α+β],r*Sin[α+β]} as {r*(Cos[α]*Cos[β]-Sin[α]*Sin[β]),r*(Sin[α]*Cos[β]+Cos[α]*Sin[β])}
Now, consider a point B, that has length 1 and angle β. B is then {Cos[β],Sin[β]}. Now if we consider the expression for point A rotated by β, we can see that it can be expressed simply as the coordinates of A and B. Namely, replace
Cos[α] by a Sin[α] by b Cos[β] by c Sin[β] by d
and we see that a point {a1,a1} having α angle, rotated by β angle, can be expressed as {a*c - b*d, b*c + a*d}, where {c,d} is a point with β angle.
Definition of Complex Numbers
A Complex Number is defined as a pair {a,b}, where a and b are real numbers.
We will sometimes use capital letters such as A, B, C to denote complex numbers. For us, the complex numbers is just a point in the plane.
Definitions of Plus and Times functions
We define two functions that can be applied to complex numbers. Plus[A,B] and Times[A,B]. Each is a function that takes two complex numbers as arguments, and returns a complex number.
As a notation convenience, we write “complexPlus[A,B]” as “A⊕B”, and we write “complexTimes[A,B]” as “A⊗B”.
complexPlus[{a,b},{c,d}] := {a + c, b + d}
complexTimes[{a,b},{c,d}] := {a*c - b*d, b*c + a*d}
We also define a function complexInversion, which gives us the multiplicative inverse of a given argument. That is, complexInversion[A] has a value such that A⊗complexInversion[A]=={1,0}. We use a circle slash ⊘ as a shorthand operator notation for complexInversion. That is, complexInversion[Z] can be written as {1,0}⊘Z:
complexInversion[{a,b}] = 1/(a^2+b^2) ⊙ {a,-b}
and we also define a negative element function, with shorthand operator syntax of ⊖Z. So that,
addictiveInverse[{a,b}] = {-a,-b}
This definition of multiplication has important meaning when interpreted geometrically. Complex numbers can be thought as vectors, with a multiplication rule.
Here's a explanation: Suppose the distance from {c,d} to {0,0} is r, and suppose it makes an angle θ with the positive x-axis. Then, a complex number {a,b} multiplied by {c,d} by the definition {a*c - b*d, b*c + a*d}, is geometrically equivalent of rotating the point {a,b} by θ, then scale it by r.
Note: above we used the concept of distance and angle. These can be defined formally. Distance can be defined using the Pythagoras Theorem, and angle can be defined using trigonometry.
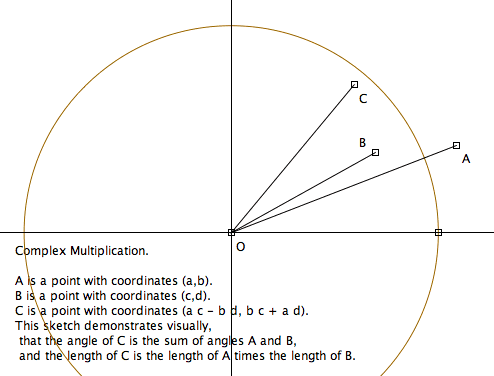
A rotation of θ around origin is expressed in complex number as multiplication by {Cos[θ],Sin[θ]}. In other words, a point {a,b} rotated by θ around the origin can be written as {a,b}⊗{Cos[θ],Sin[θ]}.
A translation by {a,b} is expressed as adding a complex number {a,b}.
Here's how to find products of rotation, using complex numbers.
A rotation of θ centered on A can be done by a sequence of:
1. translation of -A,
2. rotation of θ on origin,
3. translate it back by A.
In formulas, we have:
r[A,θ] == t[A]^-1 * r[0,θ] * t[A].
Expressed as complex numbers, the right hand side is
R (Z - A) + A
where Z is the complex number to be acted on, and R is {Cos[θ],Sin[θ]}.
Expand and collect we have
R Z + (-R+1) A
The R Z term is a rotation of Z, while the other term is a
translation. So, we have shown that a rotation on arbitrary center is
equivalent to a rotation on origin followed by a translation.
Similarly, a translation followed by a rotation on origin:
t[A] * r[0,θ]
written in complex numbers
(Z + A) R
is equal to
Z R + A R
meaning that it is equivalent to a rotation on origin followed by a
translation.
A rotation θ on a point B followed by a translation is also
equivalent to a rotation on origin followed by a translation. Witness:
r[B,θ] * t[A]
Since rotation on an arbitrary point B is equivalent to rotation on
origin followed by a translation, as show above, so we can rewrite the
r[B,θ] to be
r[{0,0},α] * t[C]
for some α and C. Thus
r[B,θ] * t[A] == r[{0,0},α] * t[C] * t[A]
This shows that a rotation on a point followed by a translation is
just a rotation on origin followed by a translation.
The exact coordinate any product of symmetry can be easily calculated
by complex numbers.
The sequence of rotations
r[{a1,a2},α] * r[{b1,b2},β]
applied to the point
{x,y}
in complex numbers is then:
(
( ({x,y} - {a1,a2}) * {Cos[α],Sin[α]} + {a1,a2} )
- {a1,a2}
)
* {Cos[β],Sin[β]}
+ {b1,b2}
In Mathematica, if we define the complex multiplication as cTimes, and
addition as cPlus:
cPlus[{a_, b_}, {c_, d_}] := {a + c, b + d}
cTimes[{a_, b_}, {c_, d_}] := {a*c - b*d, b*c + a*d}
then our sequence of rotations:
cPlus[cTimes[cPlus[cPlus[cTimes[cPlus[{x, y}, -{a1, a2}], {Cos[α],
Sin[α]}], {a1, a2}], -{b1, b2}], {Cos[β], Sin[β]}], {b1,
b2}]
Expands to:
{b1 + Cos[β]*(a1 - b1 + (-a1 + x)*Cos[α] - (-a2 +
y)*Sin[α]) - (a2 - b2 + (-a2 + y)*Cos[α] + (-a1 +
x)*Sin[α])*Sin[β], b2 + Cos[β]*(a2 - b2 + (-a2 +
y)*Cos[α] + (-a1 + x)*Sin[α]) + (a1 - b1 + (-a1 +
x)*Cos[α] - (-a2 + y)*Sin[α])*Sin[β]}