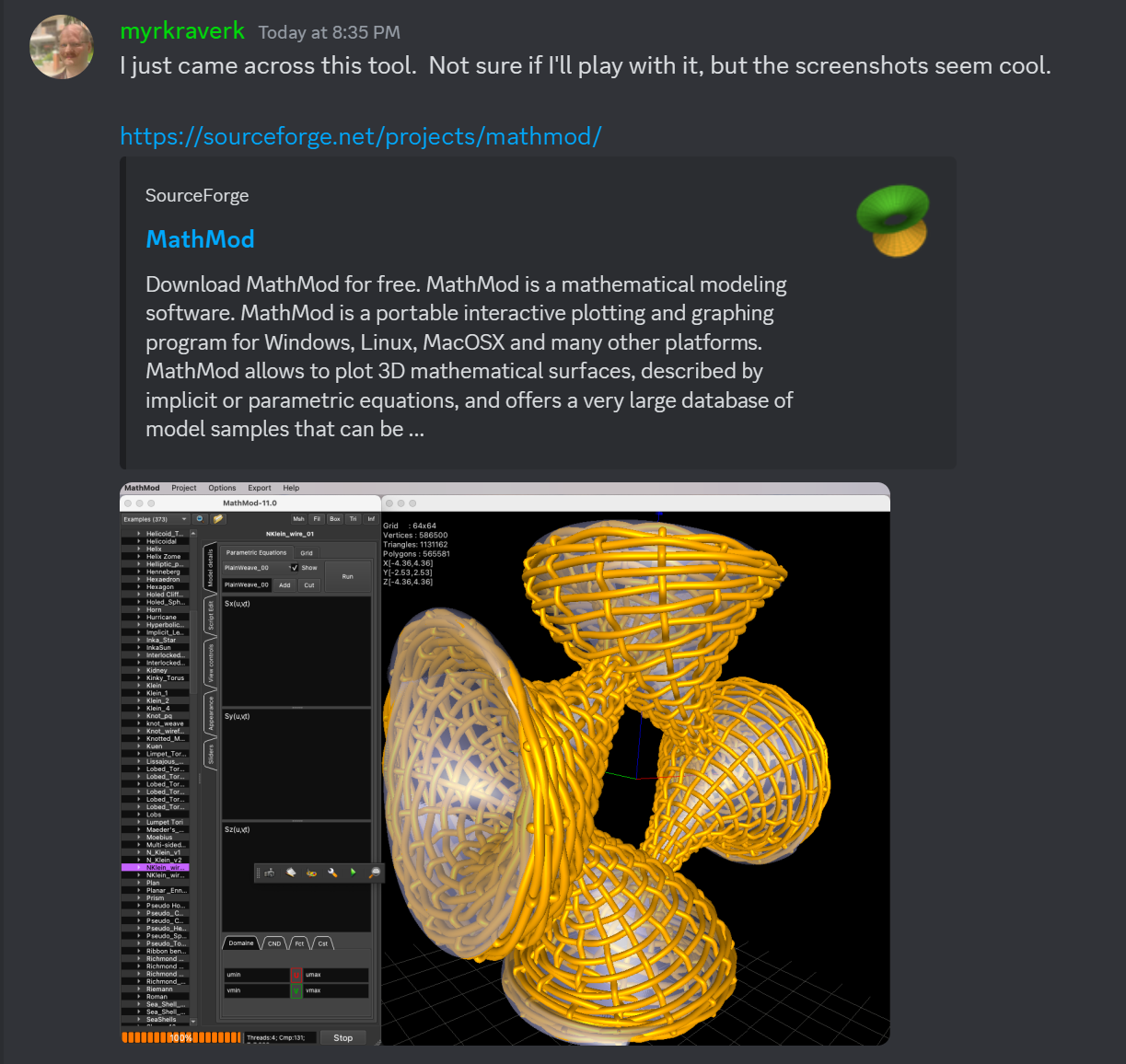
working on updating 30 years old WolframLang code that generates animation.
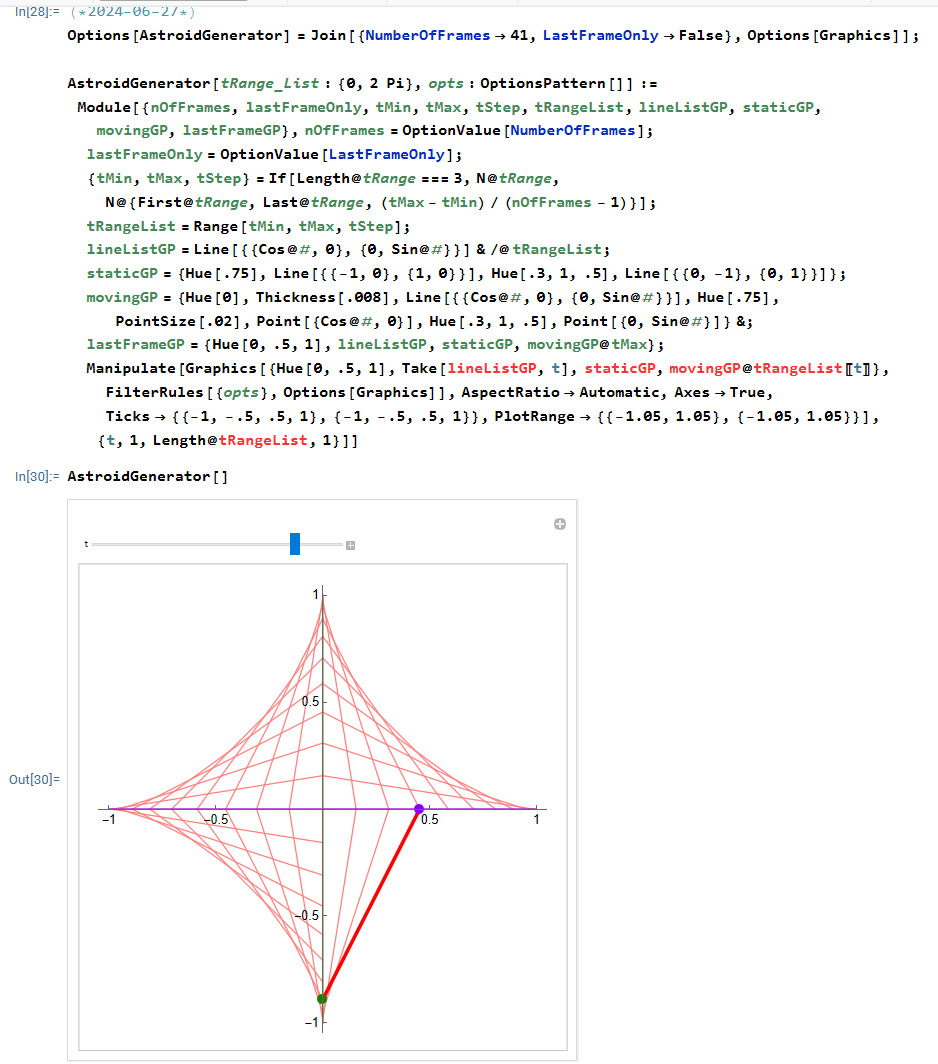
working on updating 30 years old WolframLang code that generates animation.

new edition
now on github. updated 26-years-old code. still in heavy work. but putting on github now.
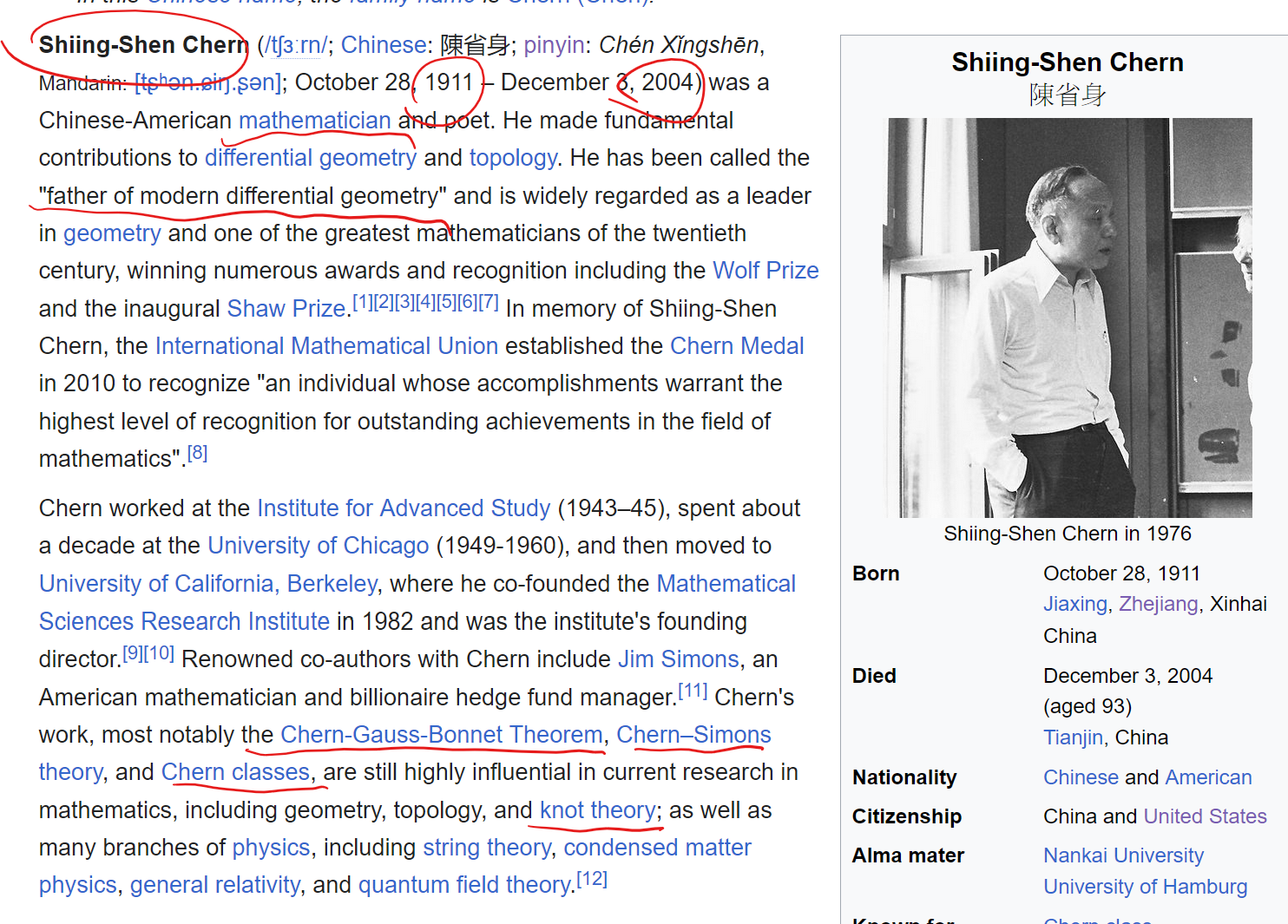
some random notes on mathematicians
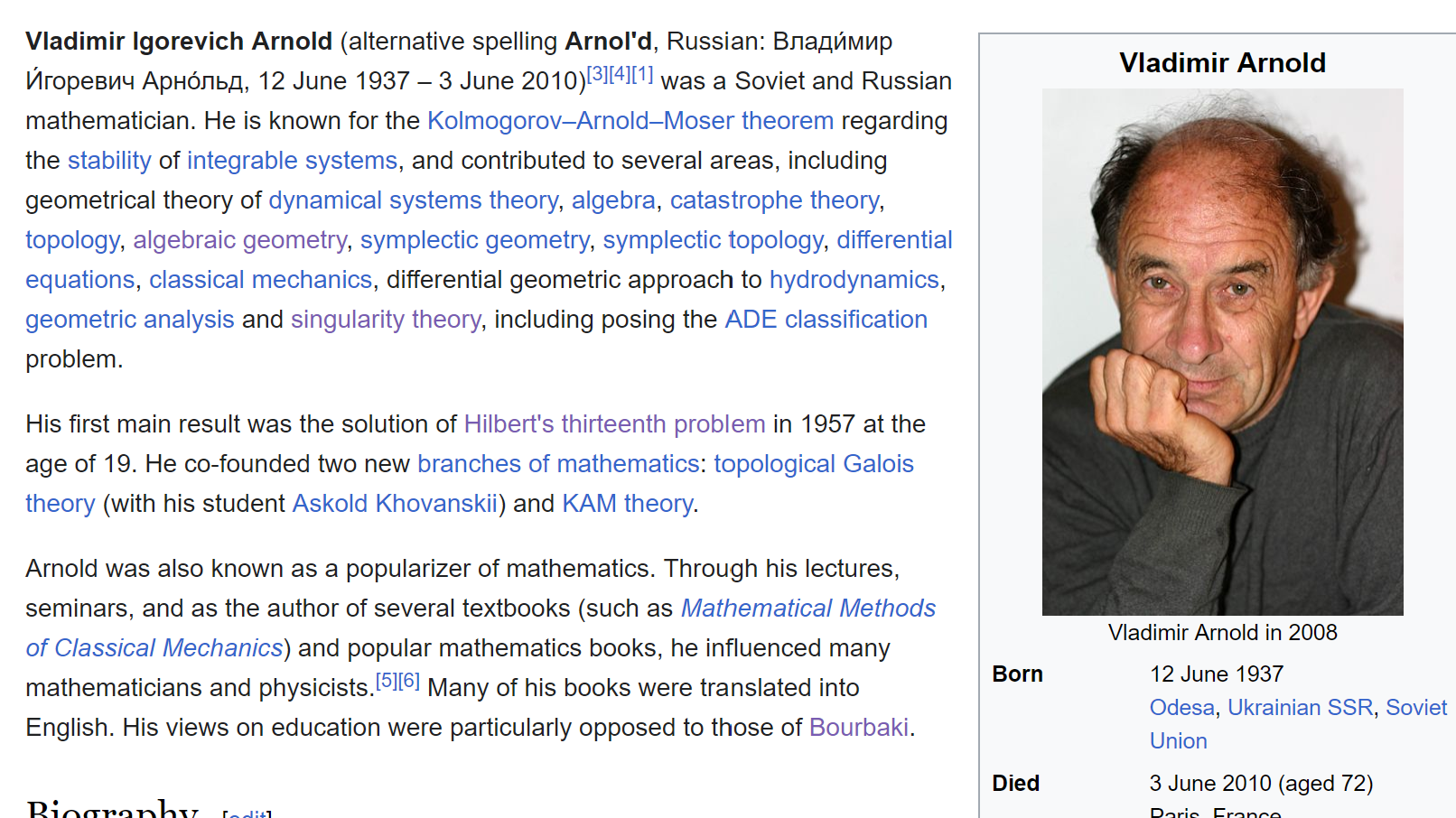
one of the great mathematician, vladimir arnold
one great mathematician Yutaka Taniyama, killed himself suicide.

lots random reading notes