In-place Algorithm, Reverse List in JavaScript, Python, Perl, Lisp, Wolfram Lang

This page tells you what's “In-place algorithm”, using {python, perl, emacs lisp, Wolfram Language} code to illustrate.

In computer science, an in-place algorithm (or in Latin in situ) is an algorithm which transforms input using a data structure with a small, constant amount of extra storage space. The input is usually overwritten by the output as the algorithm executes. An algorithm which is not in-place is sometimes called not-in-place or out-of-place.

(from Wikipedia [ In-place algorithm ] [ https://en.wikipedia.org/wiki/In-place_algorithm ])

Python 3

Here is a python code for reversing a list. Done by creating a new list, NOT using in-place:

# python3
# reverse a list, by creating new

list_a = ["a", "b", "c", "d", "e", "f", "g"]

list_length = len(list_a)
list_b = [0] * list_length

for i in range(list_length):
    list_b[i] = list_a[list_length -1 - i]

print (list_b)
# ['g', 'f', 'e', 'd', 'c', 'b', 'a']

Here is in-place algorithm for reversing a list:

# python3
# in-place algorithm for reversing a list

list_a = ["a", "b", "c", "d", "e", "f", "g"]

list_length = len(list_a)

for i in range(list_length//2):
    list_a[i], list_a[ list_length -1 - i] = list_a[ list_length -1 - i], list_a[i]

print(list_a)
# ['g', 'f', 'e', 'd', 'c', 'b', 'a']

The a//b is for integer quotient.

Perl

Here is a perl version.

# perl
# reverse a list, by creating new

use strict;
use Data::Dumper;

my @listA = qw(a b c d e f g);

my $listLength = scalar @listA;
my @listB = ();

for ( my $i = 0; $i < $listLength; $i++ ) {
 $listB[$i] = $listA[ $listLength - 1 - $i];
}

print Dumper(\@listB);

# perl
# in-place algorithm for reversing a list.

use strict;
use Data::Dumper;
use POSIX; # for “floor”

my @listA = qw(a b c d e f g);

my $listLength = scalar @listA;

for ( my $i = 0; $i < floor($listLength/2); $i++ ) {
 ($listA[$i], $listA[ $listLength - 1 - $i]) = ($listA[ $listLength - 1 - $i], $listA[$i]);
}

print Dumper(\@listA);
__END__

emacs lisp

;; emacs lisp
;; reverse a array, by creating new

(setq arrayA ["a" "b" "c" "d" "e" "f" "g"])
(setq arrayLength (length arrayA))
(setq arrayB (make-vector arrayLength 0))
(dotimes (i arrayLength ) (aset arrayB i (aref arrayA (- (1- arrayLength) i))))
(message "%s" arrayB)
;; [g f e d c b a]

;; emacs lisp
;; in-place algorithm for reversing a array

(setq arrayA ["a" "b" "c" "d" "e" "f" "g"])

(setq arrayLength (length arrayA))

(dotimes (i (floor (/ arrayLength 2)))
  (let (x)
    (setq x (aref arrayA i))
    (aset arrayA i (aref arrayA (- (1- arrayLength) i)))
    (aset arrayA (- (1- arrayLength) i) x) ) )

(message "%s" arrayA)
;; [g f e d c b a]

Wolfram Language

(*reverse a list, by creating new*)
listA = {"a", "b", "c", "d", "e", "f", "g"};
listLength = Length@listA;
listB = Range@listLength;

listB = (listB[[#]] = listA[[listLength - # + 1]]) & /@ listB

(* reverse a list, in-place. *)

listA = {"a", "b", "c", "d", "e", "f", "g"};
listLength = Length[listA];

({listA[[#]], listA[[listLength - # + 1]]} = {listA[[listLength - # + 1]], listA[[#]]}) & /@ Range@Floor[Length@listA/2];

listA

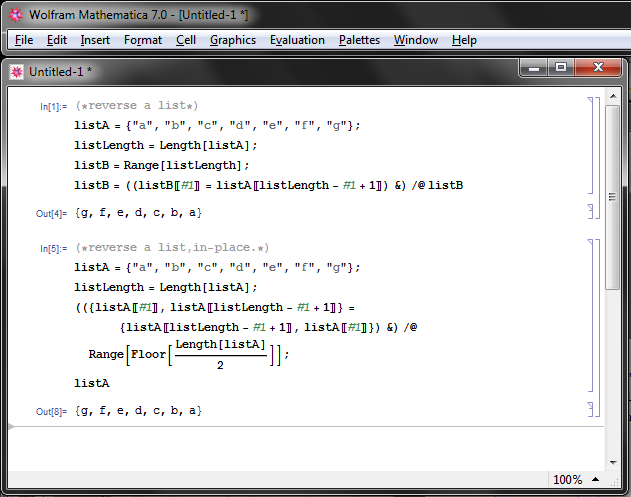
Note: in-place algorithm are not encouraged in functional programing. So, in functional language such as {lisp, Wolfram Language}, the constructs above are a bit forced. The examples here are only for illustrating the concept of in-place algorithm. All the above langs have built-in functions for reversing a list.

2012-02-29 Thanks to Steven D'Aprano, Dan Stromberg.