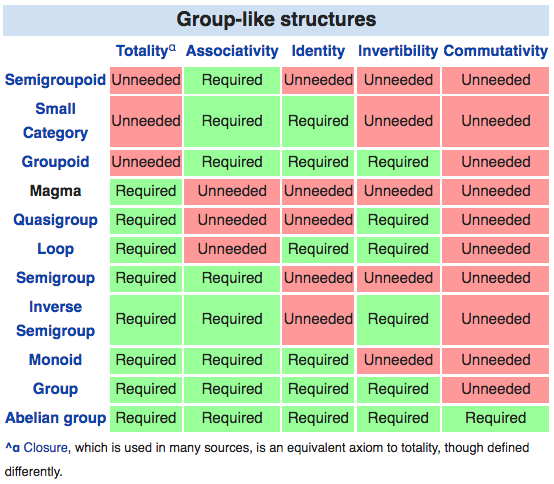
Combinatorial Exploration of Algebraic structures

it'd be something to understand the relation and consequences of these structures, as universal algebra. if reading 1 hour per day, 1 year might do.

what am afraid is, after you understand them, turns out there is no theory that unite them in a simple way, like running a cellular automata. this would be mathematician's nightmare.

looking at these properties, you wanna look into what's their nature. Or, how is it they are this or that “properties”.

the simplest is totality. Basically it means whether f[a,b] returns a element in the set. This is uninteresting. In studying structures, we of course want all operation to be closed. The reason “totality” property happens in the table is not a natural one. Rather, we have concept of total function and partial function because in some situation of math we don't know the exact domain of the function.

The other simplest is communitivity. It is a situation that happens when you have a set of at least 2 elements, and a binary operator. you have the issue whether a*b = b*a.

The nature of identify and invertibility properties are related. identity means there is a element i such that a*i=a and i*a=a. Sometimes requiring just one of them, called left identity or right identity

Inverse means for any x there is a -x such that x * -x = i and or -x * x = i

So, the concept of inverse is dependent on concept of identity.

so, to see their nature, perhaps we focus first on identity. Seems to me, the next step is to see the different of structures with identity vs without.

For associativity, it arise due to a basic situation that happens with a set of 3 or more element and a binary operation. It has to do with order of applying the operation.

See the Nature of Associative Property of Algebra

On the whole, if we look at the table again, we see that the table does not exhaustively list all combinations of properties. For example, there is no structure in the table that satisfies totality, associativity, identity, but not invertibility, communitivity.

So, we like to create a table that has all possible combination of the yes/no situation of the 5 properties list.

Then, we also note, these 5 properties do not seem exhaustive or well qualified. For example, associativity requires that the set has at least 3 elements. This condition is not explicitly stated in the table. Also, we like to find a defining quality for a property to be listed in the property list. For example, why isn't the condition of symmetric group or cyclic group or dihedral group.