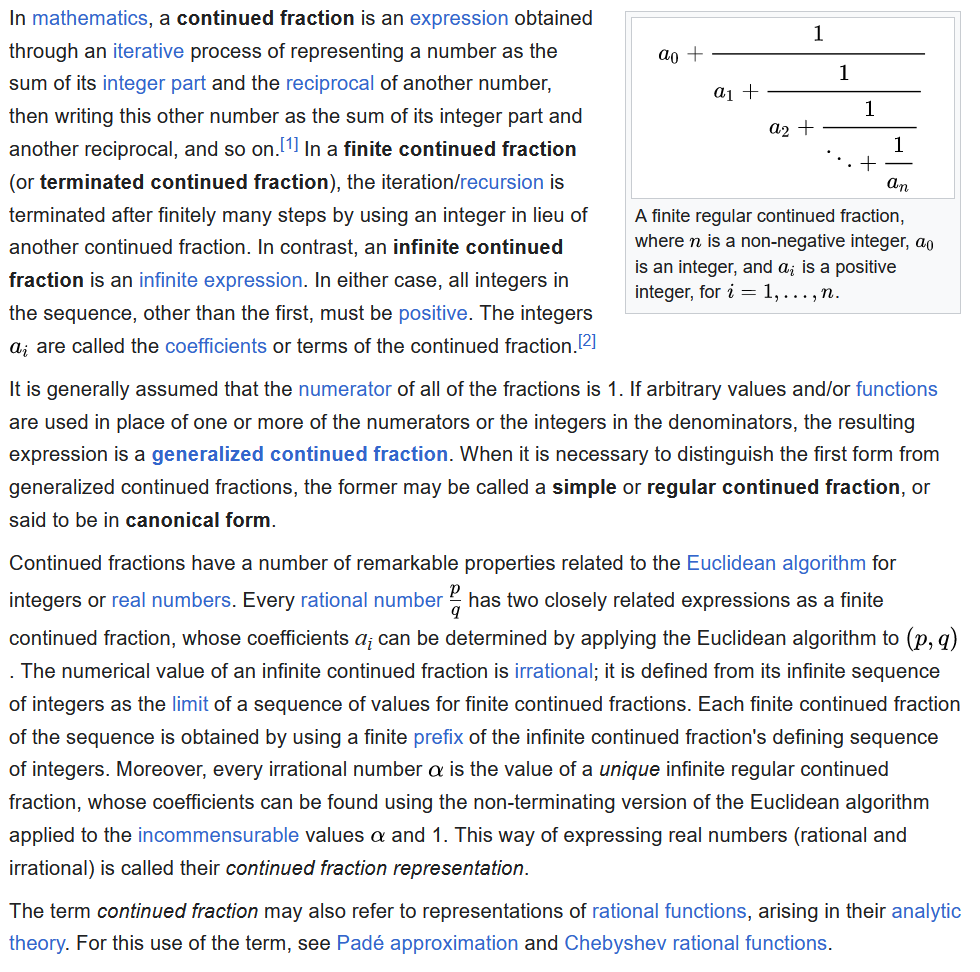
Continued Fraction

• math. continued fraction.
• Mathematician Bill Gosper made significant contribution.

• Continued fractions.
• For rational numbers, it's finite.
• For irrationals, it's infinite.
• If it repeats, it's a quadratic irrational. That is, number of the form (a + b * Sqrt[c])/d

• interesting property of continued fraction for rationals.

• https://x.com/xah_lee/status/1717760067607711887

2023-10-26

now, the incomprehensible part of continued fractions.

• Stil, interesting is quadratic rationals, dyadic rationals (binary exact numbers), Minkowski question mark function.
• And that something with Möbius transformations is super interesting.

• the cumulation of my math study today
• https://x.com/xah_lee/status/1717784384273785250

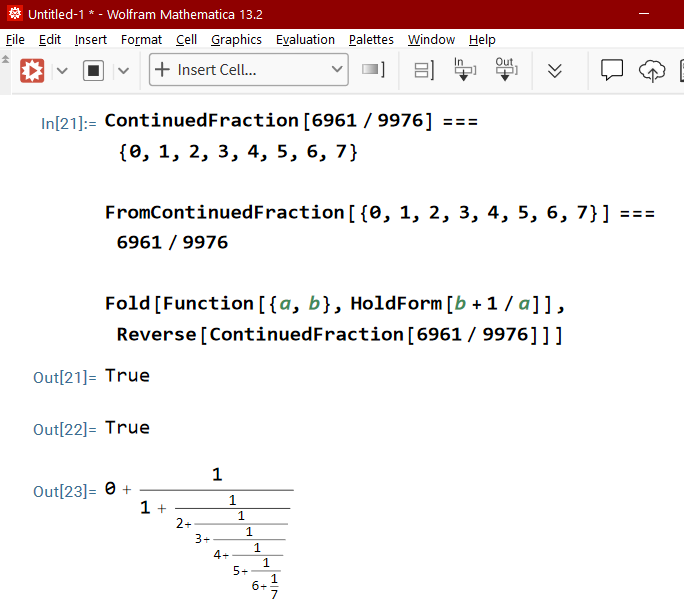
ContinuedFraction[ 6961/9976 ] === {0, 1, 2, 3, 4, 5, 6, 7}

FromContinuedFraction[ {0, 1, 2, 3, 4, 5, 6, 7} ] === 6961/9976

Fold[
Function[{a,b}, HoldForm[ b + 1/a ] ],
Reverse[ ContinuedFraction[ 6961/9976 ]  ]
]

(* typeset Continued Fraction *)
Fold[
Function[{a,b}, b + 1/a ],
Reverse[ {a,b,c,d} ]
]

(* a + (b + (c + d^(-1))^(-1))^(-1) *)

ContinuedFraction[ Pi//N ]
(* {3, 7, 15, 1, 292, 1, 1, 1, 2, 1, 3, 1, 14} *)