Geometric Inversion, 2D Tiles

geometric inversion as decorative pavement tiles

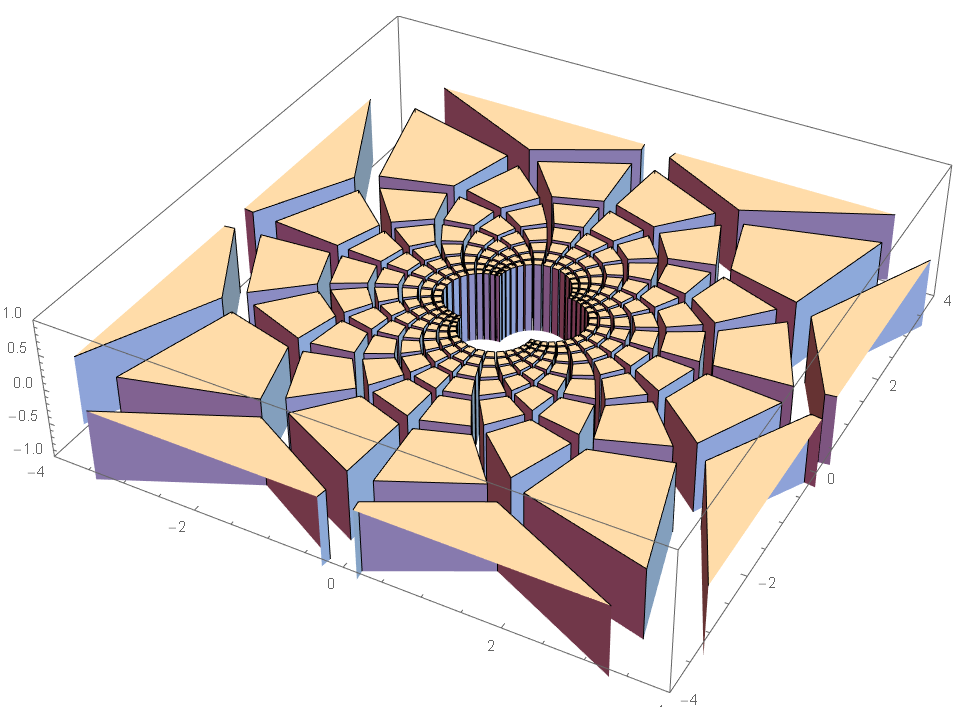
geoInv = ((With[{x662 = #.#}, If[ x662 < 0.00000001, #, #/x662] ]) &);

xRange=1;
gridDivN = 15;
δ=xRange 2/gridDivN;
sqWidth=δ * 8/10;
s=sqWidth/2;
tileHeight= -2;

squaresGP=
Table[
With[{ a={x-s,y-s},b={x+s,y-s},c={x+s,y+s},d={x-s,y+s}},
GraphicsComplex[{a,b,c,d},Line@{1,2,3,4,1}]
]
,{x,-xRange,xRange,δ},{y,-xRange,xRange,δ}];

Graphics[squaresGP, Axes -> True ]

gp2= squaresGP /. GraphicsComplex[x_, r__] :> GraphicsComplex[geoInv /@ x, r];

gp3d= gp2 /. GraphicsComplex[x_, r__] :> GraphicsComplex[ ( Append[#,0] &) /@ x, r];

Graphics3D[gp3d, Axes -> True, PlotRange-> {{-4,4},{-4,4},{-1,1}} ]

tilesGP = gp3d /. GraphicsComplex[pts_, Line[x_]]  :>
GraphicsComplex[ Join[pts,((#+{0, 0, tileHeight}) &) /@ pts],
List@Polygon@{Drop[x,-1], {1, 5, 6, 2}, {2, 6, 7, 3}, {3, 7, 8, 4}, {4, 8, 5, 1}, {5, 6, 7, 8}}
 ];

Graphics3D[tilesGP, Axes -> True, PlotRange-> {{-4,4},{-4,4},{-1,1}} ]

prevent congestion in center

because geometric inversion will swap points outside a circe to inside, so, it became very dense near the center of the circle. We want to prevent that, so garden pavement tiles don't become infinitely small.

we do this by applying the geometric inversion to grid points, also, square is also resized by the inversion. Then, we apply geometric inversion to them.

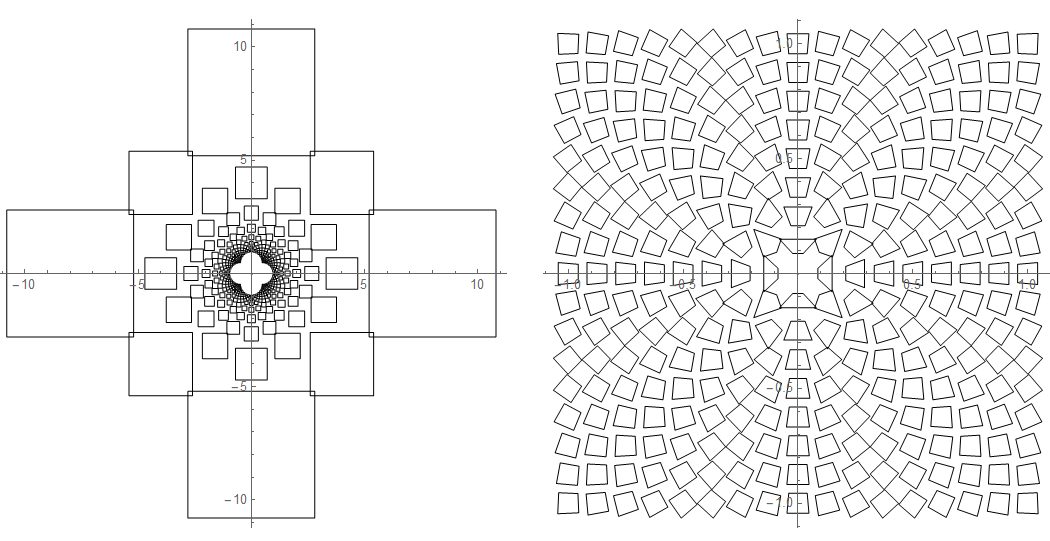
geoInv = ((With[{x662 = #.#}, If[ x662 < 0.00000001, #, #/x662] ]) &);

gridDivN = 16;
nGon = 4;
rr = (2/gridDivN) /2 (Sqrt@2) .7;
α = 2 Pi/8;

gridPoints = Map[ geoInv , CoordinateBoundsArray[{{-1,1},{-1,1}}, Into@gridDivN], {2}] ;

gp1=
With[{sq= ((({Cos[#] , Sin[#]} rr) &) /@ Range[α, 2 π+α - 2 π/nGon/2, 2 π/nGon ]) },
Map[ Function[{x}, GraphicsComplex[ ((x+#) &) /@ (sq x.x), Line @ Append[Range @nGon,1] ]],
gridPoints
,{2}]
];

gp2= gp1 /. GraphicsComplex[x_, r__] :> GraphicsComplex[geoInv /@ x, r];

gr1 = Graphics[gp1, Axes->True ]
gr2 = Graphics[gp2, Axes->True ]

GraphicsGrid[ {{gr1, gr2}} ]

3d tile

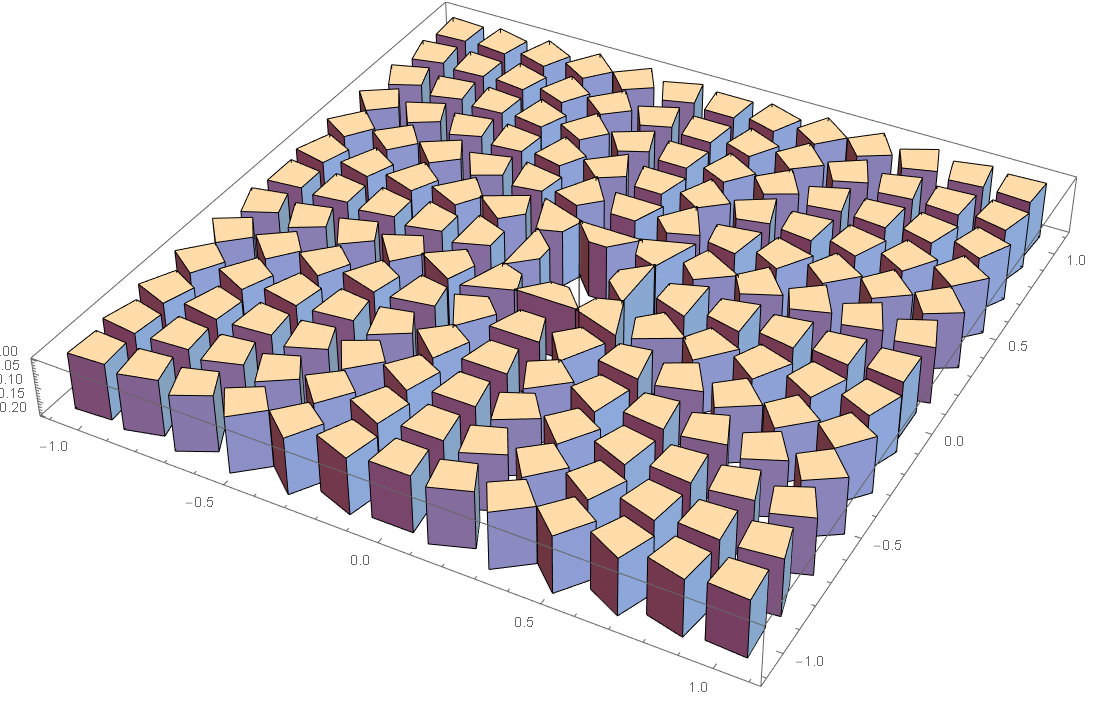
geoInv = ((With[{x662 = #.#}, If[ x662 < 0.00000001, #, #/x662] ]) &);

gridWidth = 2;
gridDivN = 14;
polygonRadius = gridWidth/gridDivN/2 .7;
polygonNumSides = 4;
polygonRotate = 2 Pi/8;
tileHeight = -0.2;

gridPoints = Map[ geoInv , CoordinateBoundsArray[{{-gridWidth/2, gridWidth/2}, {-gridWidth/2, gridWidth/2}}, Into@gridDivN], {2}] ;

polygonVertexes = ((({Cos[#], Sin[#]} polygonRadius Sqrt@2)&) /@ Range[polygonRotate, 2 π+polygonRotate - 2 π/polygonNumSides/2, 2 π/polygonNumSides]);

gPolygons2D = Map[
Function[{pt},
GraphicsComplex[ ((pt+#) &) /@ (polygonVertexes (pt.pt)), Line @ Append[Range@polygonNumSides, 1] ]],
 gridPoints, {2}];

Graphics[gPolygons2D, Axes -> True ]

g2GeoInvert = gPolygons2D /. GraphicsComplex[pts_, r__] :> GraphicsComplex[geoInv /@ pts, r];

Graphics[g2GeoInvert, Axes -> True ]

g3D = g2GeoInvert /. GraphicsComplex[x_, r__]:>GraphicsComplex[( Append[#, 0]&) /@ x, r];

Graphics3D[g3D, Axes -> True]

g4Tiles3D = g3D /. GraphicsComplex[pts_, Line[indexes_]]  :>
GraphicsComplex[
 Join[pts, ((#+{0, 0, tileHeight}) &) /@ pts],
 Polygon@
With[{
 polyTop = Range[polygonNumSides],
rangeX = Partition[ Append[Range[polygonNumSides], 1], 2, 1],
 polyBottom = Range[polygonNumSides+1, 2 polygonNumSides]
},
Join[
 {polyTop},
((With[{x = First@#, y = Last@#}, {x, y, y+polygonNumSides, x+polygonNumSides}] &) /@ rangeX ),
{polyBottom}
]
]
];

Graphics3D[g4Tiles3D, Axes -> True]