Geometric Inversion, Wolfram Code
-
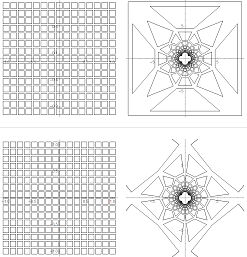 Geometric Inversion, 2D Grid
Geometric Inversion, 2D Grid -
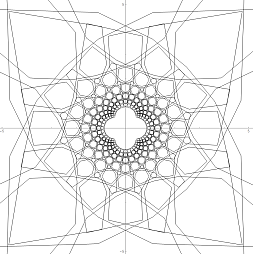 Geometric Inversion, 2D Grid, Polygon
Geometric Inversion, 2D Grid, Polygon -
 Geometric Inversion, 2D Tiles
Geometric Inversion, 2D Tiles -
 Geometric Inversion, 3D Tubes
Geometric Inversion, 3D Tubes -
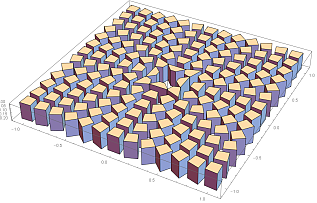
 Geometric Inversion, 3D Cubes
Geometric Inversion, 3D Cubes
ideas for pretty graphics with geometric inversion
geometric inversion can be applied to points in 2d or 3d. or higher dimension and project to 2d or 3d.
first, for 2d, it can start on grid points.
the grid points can be spheres, or lines connecting on grid points, or tube connecting them.
or, we can have square patches centered at the grid points.
the grid points can be hexagonal, or arbitrary regular tilings.
the object on the grid points, can be square, or other regular polygon, or lines/tubes connecting the points.
For 2d case, we can add height so they became 3d tiles.
we can also try to prevent congestion in the center.
3d case
Now, for 3d case, all the above variations.
- grid points can be regular grid, or any 3d regular tiling points.
- points can connected by tube.
- points can represented by spheres, or cubes, or other fitting regular polyhedron. e.g. octahedron. the octahedron can itself be decorated. e.g. have face open, or as tubes, or truncated, stellated, etc.
also, the starting points can be mapped to prevent congestion in center.
Video Tutorial
