By Xah Lee. Date: .
Variations with Different Connection of Cube Vertexes
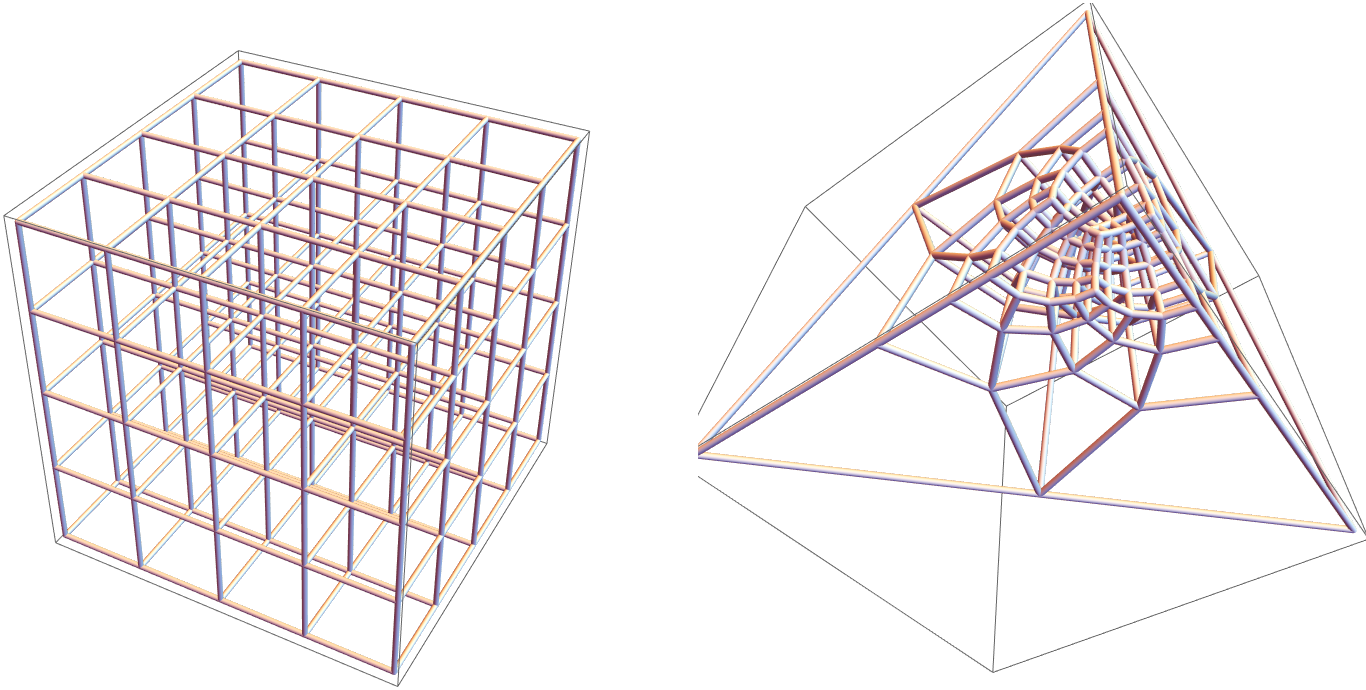 geometric inversion 3d tubes 2023-02-21 Cfjm6
geometric inversion 3d tubes 2023-02-21 Cfjm6
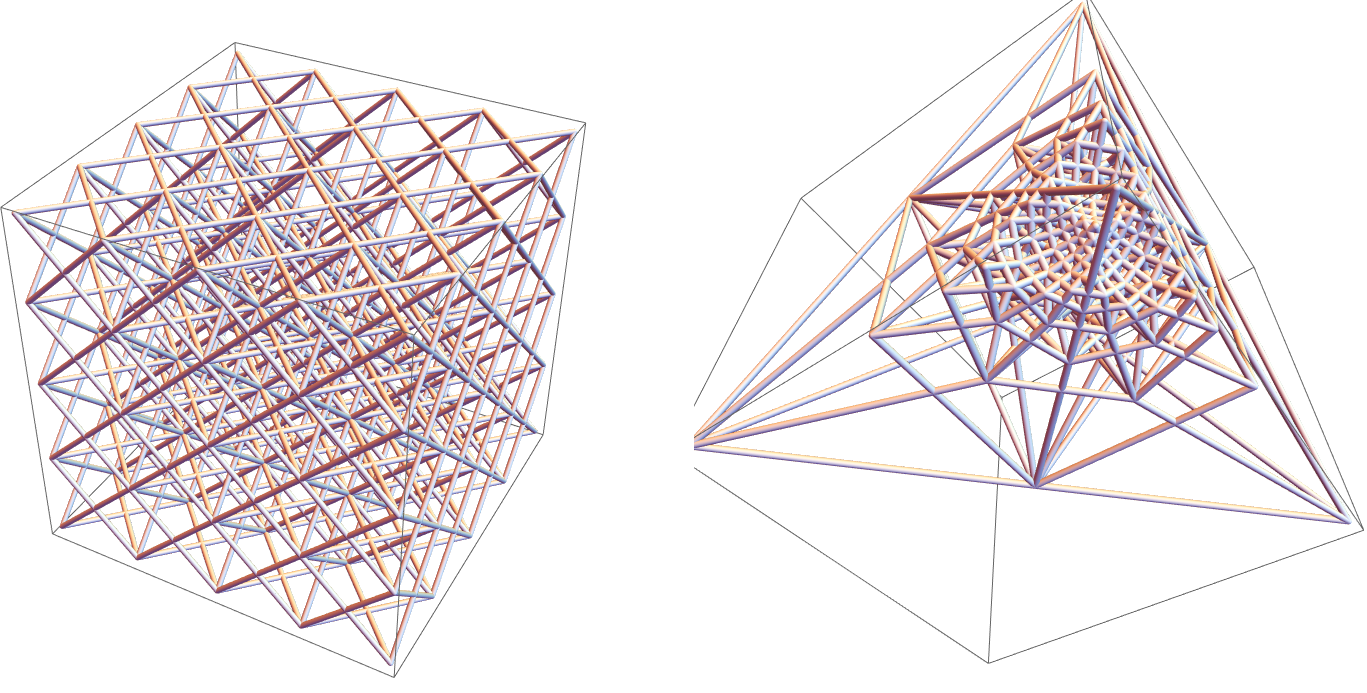 geometric inversion 3d tubes 2023-02-21 GVBT8
geometric inversion 3d tubes 2023-02-21 GVBT8
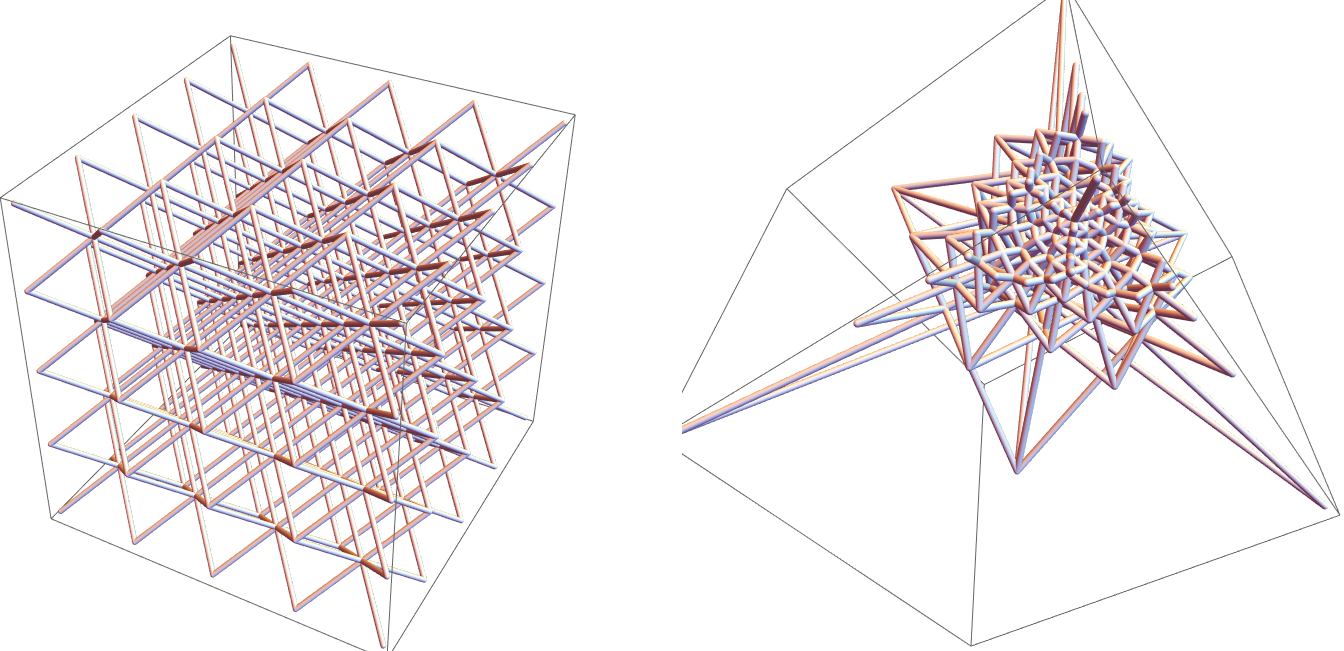 geometric inversion 3d tubes 2023-02-21 GSVPN
geometric inversion 3d tubes 2023-02-21 GSVPN
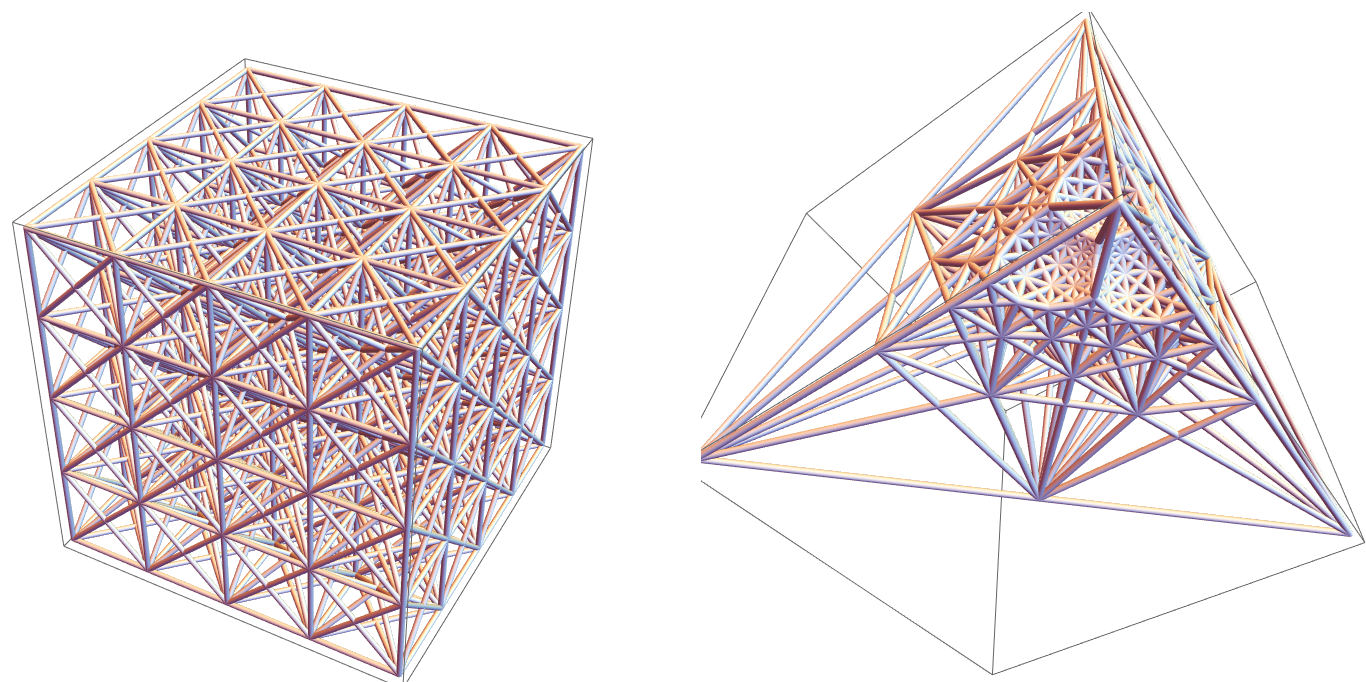 geometric inversion 3d tubes 2023-02-21 4c4ng
geometric inversion 3d tubes 2023-02-21 4c4ng
Clear[ geoInv, fCubeCorners, fTubeCube ];
geoInv = ((With[{x662 = # . #}, If[x662 < 0.00000001, #, #/x662]]) &);
fCubeCorners[{x_, y_, z_}, s_] := Tuples @ Transpose[ {{x, y, z}, {x, y, z}+ s} ]
fTubeCube[{x_, y_, z_}, s_] := Tube /@ Subsets[ fCubeCorners[{x, y, z}, s], {2} ]
xgrid = CoordinateBoundsArray@ Table[ {0,3}, {3}];
tAll = Map[ ((fTubeCube[#,1]) &), xgrid, {-2}];
tBox = Cases[ tAll, Tube[{a_, b_}]/;((EuclideanDistance[ a, b ] === 1) ),{-4}];
tfaceDiag = Cases[ tAll, Tube[{a_, b_}]/;((EuclideanDistance[ a, b ] === Sqrt[2]) ),{-4}];
tCross = Cases[ tAll, Tube[{a_, b_}]/;((EuclideanDistance[ a, b ] === Sqrt[3]) ),{-4}];
v1 = Replace[ tAll, {x_, y_, z_} :> geoInv[{x, y, z}], {-2}];
v2 = Replace[ tBox, {x_, y_, z_} :> geoInv[{x, y, z}], {-2}];
v3 = Replace[ tfaceDiag, {x_, y_, z_} :> geoInv[{x, y, z}], {-2}];
v4 = Replace[ tCross, {x_, y_, z_} :> geoInv[{x, y, z}], {-2}];
Graphics3D[ tAll ]
Graphics3D[ tBox ]
Graphics3D[ tfaceDiag ]
Graphics3D[ tCross ]
Graphics3D[ v1, ViewVector -> {-.5, -.2, -1} ]
Graphics3D[ v2, ViewVector -> {-.5, -.2, -1} ]
Graphics3D[ v3, ViewVector -> {-.5, -.2, -1} ]
Graphics3D[ v4, ViewVector -> {-.5, -.2, -1} ]
GraphicsGrid[ {{Graphics3D @tAll, Graphics3D[ v1, ViewVector -> {-.5, -.2, -1} ]}} ]
GraphicsGrid[ {{Graphics3D @tBox, Graphics3D[ v2, ViewVector -> {-.5, -.2, -1} ]}} ]
GraphicsGrid[ {{Graphics3D @tfaceDiag, Graphics3D[ v3, ViewVector -> {-.5, -.2, -1} ]}} ]
GraphicsGrid[ {{Graphics3D @tCross, Graphics3D[ v4, ViewVector -> {-.5, -.2, -1} ]}} ]





