Reading Notes on “The Shape of Space”

Notes on Jeff Week 's book

Note: this is unpolished personal note. It may contain errors, incomplete thoughts, or even unfinished sentence.

Attributes of space:

• topology vs geometry
• global vs local
• homogeneous vs non-homogeneous
• intrinsic vs extrinsic
• open vs closed.

These words describe certain attributes of spaces. For example, the local geometry of a sphere is the same as a plane. A plane or sphere is a homogeneous space since the geometry is everywhere the same, while a torus or monkey saddle surface is not. A closed one-dimensional space of a circle is different from a knot extrinsically, but are identical when considered intrinsically.

I wanted to define or categorize these terms in some mathematical way, and finding it not easy. For example, are these terms merely descriptive and used as a convenience in communication, and or are some of them characterize some important intrinsic mathematical concepts such as dimension, and if so, what are other terms of the same class or hierarchy? I think these terms are descriptive than as some intrinsic math properties or attribute designations (such as dimension). The closest having intrinsic math content is the “closed” or “open”, but then these words when used on spaces or manifolds there are 2-manifolds that are finite in area but infinite in extent.

intrinsic vs extrinsic: topology has a intrinsic or extrinsic aspects. For example, compare a rubber band, and the same band that is cut and reconnected by two half twists. They have the same intrinsic topology, because a creature on the surface has no way to tell their difference. However, their topology are extrinsically different.

Two surfaces have the same intrinsic topology if Flatlanders living in the surface cannot (topologically) tell one from the other. Two surfaces have the same extrinsic topology if one can be deformed within three-dimensional space to look like the other.

Geometry can also has intrinsic and extrinsic aspects. A piece of flat paper vs it rolled up into a cylinder shape. On both, A straight line from A to B will be the same.

I think much video games can be introduced with these ideas, largely unexplored because few people knew them. Though, much thinking needs to be done to imagine a enticing game.

The term “straight” is given as the “shortest path between two points” known as “geodesics”. So, is that all there is to “straight”? That is, it must involve two points? If so, then common usage of the term straight may need some explanation. For example, on a sphere, we know that if we just go straight in any direction we'll return to the starting point. However, if “straight” is replaced by “geodesics” than the sentence no longer makes sense because it didn't give two points. This demonstrates that the concept of straight as used daily in math is mathematically more than just “shortest distance between two points”.

concept or phrase of “straight”

The concept of mirror or flipped is also intriguing. If we look at the mirror, we see the left and right side flipped. However, why left-and-right, not up and down? Is mirroring has some special property about the horizontal line? or directional? or has it to do with gravity? Apparently not. The answer to the paradox lies in that we are observing a spacial-orientation-reversal thru a 2-d observation. That is, we look at the mirror, which is a 2-d reflection of a 3-d object, and we are (incorrectly) equating this mirror-image as a true 3-dimensional flip. If a person went thru 4th dimension and return flipped, not only his left and right sides are swapped, but also front and back, up and down. Because we are used to gravity, we would rotate or re-orient ourselves in so that we can compare our old self head to head and toe to toe and side by side for better comparison. Because human beings has bi-lateral symmetry, thus we immediately see that our left and right are reversed, forgetting that up and down and front and back are also reversed. In short, reflection thru a mirror is only a 2-d flip, not a 3-d flip.

Among these 2d spaces, there's the idea of orientability, which is a intriguing property: that it is possible to move about in the space and become mirror image. I want to say by moving in a straight line one can become a mirror image, but then one needs to define “straight”. Straight is easy to define in a homogeneous space i think, but conceivable what if we have a non-orientable space that does not have a homogeneous representation? When moving in a path that returns flipped, such path is call orientation-reversing path. What is the nature of such path? Such statements seems to imply that there are something special about certain part of the space that is special as to reverse thing's orientation. But i think in a homogeneous representation there is no part of the space that is special, so just about every straight movement becomes a orientation. Then again, in a square as Klein bottle with top and bottom edges glued and left and right flip-glued, apparently moving vertically does not reverse orientation. So, the question on the nature of orientation-reversing path is so far not understood by me.

2D manifolds

Some closed 2D manifolds:

* sphere, S2
* torus, T2, can be represented by a square with opposite edges glued
* Klein bottle, K2, square with two edge flipped
* projective plane, P2, hemisphere with opposite points on edge glued

Torus is like a donut shaped surface. Torus is also topologically equivalent to a square where the top and bottom edges 'glued' and left and right edges 'glued', so that if a point moves off the upper right edge, it reappear on the upper left edge. Similarly, if a point moves off the right top edge, it reappear on the right lower edge.

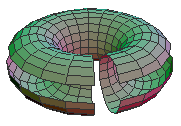
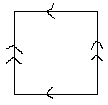
The Classification Theorem

Every surface is a connected sum of tori and or projective planes. More specifically, every surface is either a sphere, or a connected sum of either tori only, or projective planes only.

creating manifolds by abstractly gluing opposite sides of polytopes

It seems various space can be made by gluing the sides of a regular polytope (having even sides) that tiles the space. In 2-space with a square, we have T2, K2, P2, with 0, 1, 2 sides reversed respectively. What 2-manifold do we get if we try hexagon? Similarly, a cube with opposite sides glued we have T3. Reverse a side we have K3.

A hexagon with appropriate edges glued can become a torus. e.g. {1,2,3,-1,-2,-3} (go clockwise on the side of a hexagon, positive and negative indicate direction, number is label. Sides of the same number are to be glued.) With 2 points where 3 corners meet.

A square with opposite edges reversed glued is a project plane? But there are 2 points where 2 corners meet. These points are called cone points. Cone points happen whenever sum of the angles at a point is less than 360.

It can be such that the degree of a corner adds up to more than 360. That's called the opposite of a cone point.

The hexagon torus and square torus have the same local geometry: flat. However, they have different global geometry. This can be seen by tiling them to see what line of sight will be. (i don't quite understand the concept of global geometry here)

* P2 with a disk cut open is the Mobieus Strip.
P2+P2 = K2

I don't quite understand the topological difference between K2 and
P2. Perhaps because one has a special orientation-reversing path. This
would imply that K2 is not the same everywhere or is somehow
directional.

* the book mention isotropic. Quote: “A isotropic manifold is one in which the geometry is the same in all directions. S^2*S^1 is not isotropic because some 2-d slices have the local geometry of a sphere, while other slices have the local geometry of a plane, as we have discovered in the proceding two paragraphs. (The distinction between homogeneous and isotropic manifolds is not readily apparent to most Spacelanders because of the peculiar fact that there are no surfaces that are homogeneous but not isotropic.)”

I don't quite understand the above. The S^2*S^1 is represented as follows: imagine a thick sphere. In other words, a hollow solid sphere. Now imagine the inner wall of the sphere are connect to the outer wall. This is one way to imagine S^2*S^1. Now, any "skin" or "skin layer" is a 2d slice of this manifold. But we can also take the plane as it cuts thru the sphere. These two 2D slices has different geometry. One spherical, one flat. That's why the author mentions isotropic.

I do not quite understand it because it's not clear to me how geometry is defined, and how it is ok to apply to this mental image. Also, what happens if the slice is slanted? doesn't it imply there are infinity number of geometries on S^2*S^2 then?

* also, since a torus can be represented in a plane by a square, why
 cannot a sphere be represented as a plane with a point at infinity thru
 stereographic projection? how about P2 on a square?

Gauss-Bennet formula

* triangle on sphere of radius one has area (α+β+θ) - π
* sphere of radius 1 has area 4*π.
* a convex polygon with n sides can be broken into n-2 triangles.
* a convex polygon with n sides has total interior angles of (n-2) π.
* a convex polygon with n sides has total area of Sum[an tttttttt,{i,1,n-2}].
* for a sphere of radius one, broken into “cells”, we can come up with
a formula that relates it's areas with the number of edges, vertices,
faces of the cell. First image the cell edges are geodesics. Then,
each cell can be considered as a polygon, thus having n-2 triangles,
which we can computer its area.

Let
f denote the total number of faces in the cell division.
v denote the total number of vertices in the cell division.
e denote the total number of edges in the cell division.
faceArea[i] denotes the area of ith face.

Total Area = Sum[faceArea[i],{i,1,f}]

For each face, it's area can be computed by breaking down into triangles:

Let triangleAnglesSum[i,j] denote the angle sum of ith triangle in jth face.

faceArea[i] = Sum[triangleAnglesSum[j] -π, {j,1,n-2}] =
Sum[triangleAnglesSum[j], {j,1,n-2}] - Sum[π, {j,1,n-2}] =

 ((α+β+θ) - π)(n-2) = angleSum n - 2 angleSum - n π + 2 π = angleSum[1] (n-2) + (-n+2) π

connection of Topology and Geometry

in chapter 11, it is explained (a theorem) that every surface can be given a homogeneous geometry. And, a surface cannot have more than one homogeneous geometry. Example: Sphere has homogeneous elliptical geometry, donut has homogeneous flat geometry, and surfaces with more than one handles has homogeneous hyperbolic geometry. What about sums of P^2? Projective plane has homogeneous elliptical geometry. Klein bottle (= P^2+P^2) has homogeneous flat geometry. What about others involving the projective plane?

Answer:

closed surfaces and their homogeneous geometry

          | orientable | non-orientable
elliptic  |     S^2    |   P^2
Euclidean |     T^2    |   K^2
hyperbolic| all the rest surfaces

various 3D manifolds

So far these 3-manifolds are discussed:

• T3 (3-torus), T2*S1: A cube where opposite walls are connected. Alternatively, a thick torus with inside wall connected to outside wall.
• K2*S1: cube where opposite walls are connected, but one pair of opposite walls are flipped.
• cube where opposite walls are connected, but one pair of opposite walls are turned one-quarter. (page 109)
• S2*S1: thick sphere with a hollow, with the inside wall connected to outside wall. (page 95)

One-sidedness vs Non-orientability

I am surprised to learn in chapter 8, that one-sidedness and non-orientability are not mathematically the same thing. They happens to correspond in orientable 3-manifolds. But in non-orientable 3-manifold, a surface can be 2-sided yet non-orientable, and vice versa. A simple example is a plane inside a K2*S1 manifold represented as a cube with one flipped connected sides. Depending how the plane is situated. If the “plane” is situated such that its edge is the axis of the mirror line for the flipped sides, than this “plane” is one-sided, yet orientable. Now if the plane is situated so that its edge is perpendicular to the mirro axis on one of the flipped sides, than it is non-orientable and two-sided.

Question: i was trying to think about what kind of surface is this “plane” so formed as a slice of 3-manifold. How are they as connected sums?

relation of Spherical Triangle and its Area

The area of a triangle on a sphere is A = r^2 * ((α + β + θ)-π). Given that the area of a sphere of radius 1 is 4*π. Given any two great circles, they intersect with two angles α and β. Let the smaller one be α, and we know α+β=π. The two great circles cuts the sphere into 4 areas. Two of the areas are identical corresponding to angle α, and the other two with β. The area enclosed by the two α sectors would be a fractional of the sphere. So the area of the double lune is ((2*α)/(2*π)) * 4*π, simplifies to 4*α.

now, given a spherical triangle. Since it's a triangle, it's sides must be straight (geodesics). Therefore, its sides are 3 great circles. Each two great circle form a pair of lunes. Think of the triangle as 3 pairs of lunes. Lunes are formed by two great circles, so they have a antipodal point. So, another triangle is formed on the opposite side, being symmetric to the given triangle with respect to the center of the sphere. The area of the 3 double lunes covers the whole sphere outside of the triangles, plus 3 times on each of the two triangle. In other words, it covers the whole sphere plus 4 times the area of the given triangle. So, we sum the 3 areas of the lunes (4*α+4*β+4*θ), then minus the whole sphere 4*π, would be equal to 4 times the area of the given spherical triangle. That is,

(4*α+4*β+4*θ) - 4*π == 4*A
(α+β+θ) - π == A

In the above, we assumed that the radius of the sphere is 1. For a sphere with radius r, the formula is then A = r^2 ((α+β+θ) - π).

Some materials from Chapter 10: that there are 3 types of homogeneous 2-d geometries: hyperbolic, elliptic, Euclidean. Hyperbolic has negative curvature, and elliptic has positive curvature, and Euclidean is flat, 0 curvature.

here's a way to make a paper model of the hyperbolic plane. Cut lots of equiangular triangles. Tape them together so that every vertex has 7 triangles. This forms a model of the hyperbolic plane. Note that hyperbolic plane is homogeneous, so there is no intrinsic “center”. I would like to construct this model, since it's hard to imagine it, and how it is homogeneous. If each vertex has 5 triangle, than one constructs the icosahedron, which approximate the sphere, which has elliptical geometry.

From the Optiverse website:

It was a surprising consequence of an abstract mathematical theorem of Steve Smale [Sma] that a spherical surface can be turned inside out without tearing or creasing, if we do allow the surface to pass through itself.

There is a surprising math theorem that says one can turn a sphere inside out without creating a crease. Explanation: We want to turn a sphere inside out. The sphere is rubber like, and we can deform it anyway we like, but no tearing. Also, we allow the wall to pass itself. Normally, we'd think just pull one end thru the other, and the sphere will be inside out. However, this process creates a kink. That is, before the sphere is inside out everywhere, there is a ring of "loop". The question to mathematicians is that, is it possible to message and deform and push around the sphere somewhat, so that the eversion process is smooth and never creates any kink?

Steve Smale proved a theorem in 1958 that means it is possible, to the amazement of fellow mathematicians. The proof is abstract technical and is all math formulas and does not give a explicit description of the process. Subsequently, people have tried to find a process and make a video visualization, and several are found and done over the years. John M Sullivan at University of Illinois et al is the latest group of people having created such visual demonstration: http://new.math.uiuc.edu/optiverse/. Even with this latest lucid video, it takes some persistent effort to see what is going on.

The interesting thing is that it is impossible to do this in 2-dimensional analogue. That is, turn a circle inside out without kink.