What is Riemann Surface? Understanding the Concept Without Math
in 20 years since i heard the term Riemann surface, today i finally understand it.
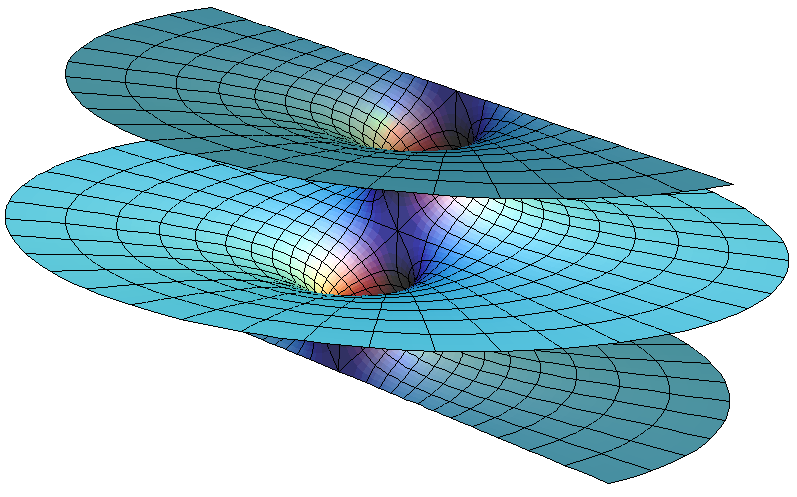
In complex analysis, a Riemann surface is a one-dimensional complex manifold. Riemann surfaces can be thought of as “deformed versions” of the complex plane: locally near every point they look like patches of the complex plane, but the global topology can be quite different. For example, they can look like a sphere or a torus or a couple of sheets glued together.
The main point of Riemann surfaces is that holomorphic functions may be defined between them. Riemann surfaces are nowadays considered the natural setting for studying the global behavior of these functions, especially multi-valued functions such as the square root and other algebraic functions, or the logarithm.
Every Riemann surface is a two-dimensional real analytic manifold (i.e., a surface), but it contains more structure (specifically a complex structure) which is needed for the unambiguous definition of holomorphic functions. A two-dimensional real manifold can be turned into a Riemann surface if and only if it is orientable and metrizable. So the sphere and torus admit complex structures, but the Möbius strip, Klein bottle and projective plane do not.
Geometrical facts about Riemann surfaces are as “nice” as possible, and they often provide the intuition and motivation for generalizations to other curves, manifolds or varieties. The Riemann–Roch theorem is a prime example of this influence.
basically, a Riemann surface is simply just a surface, as far as the shape is concerned. Any normal surface you can think of (For example, plane, sphere, torus, etc) are all Riemann surfaces. We say it's Riemann surface, is due to the context, is that we define the surface using complex functions, and for use in studying complex functions.
a Holomorphic function is:
A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain. The existence of a complex derivative in a neighborhood is a very strong condition, for it implies that any holomorphic function is actually infinitely differentiable and equal to its own Taylor series.
basically, it just means it's smooth.