Great Software for Dynamical Systems
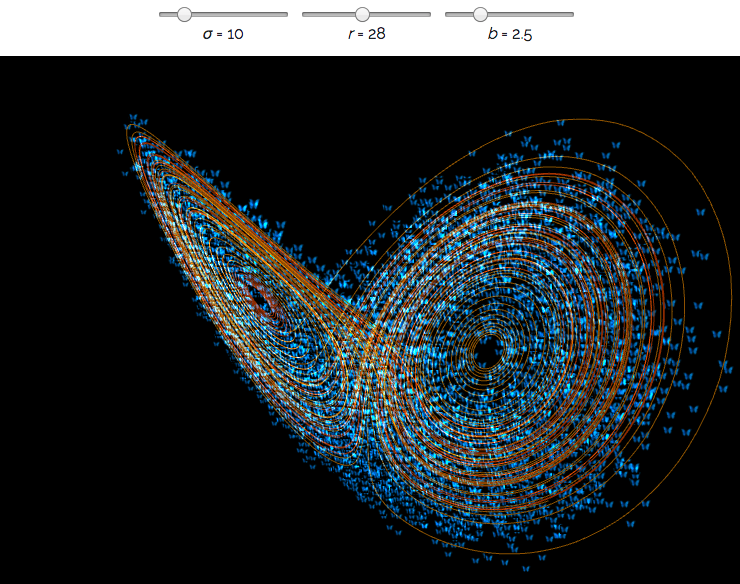
Interactive Lorenz Attractor
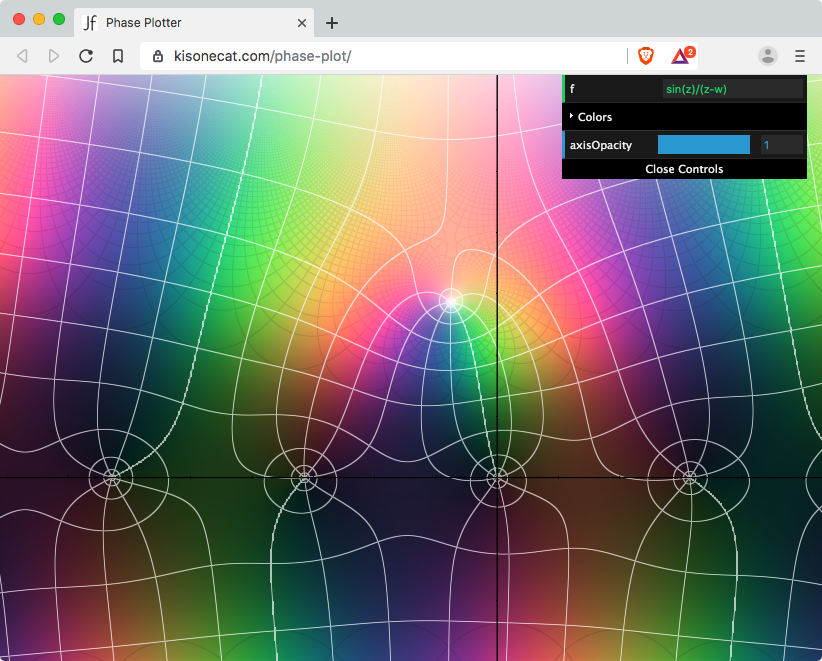
Phase Plot By Jim Fowler (Dynamical System)
StdMap
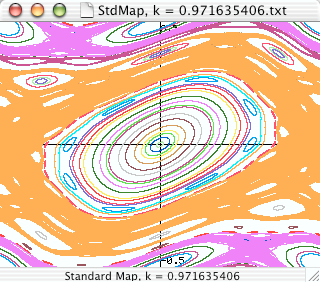
StdMap. Standard Maps displays the dynamics of several area preserving mappings. It will also find periodic orbits, cantori, and stable and unstable manifolds of any (symmetric) periodic orbit.
The program is written by mathematician J D Meiss.
1DMap
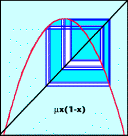
1DMap is another program by mathematician J D Meiss. It plots orbit maps of various equations, including: logistic, cosine, cubic, exp, tangent, tent, circle. For each, one can plot the correspondig cobweb, bifurcation diagram, and other statstical diagrams. The program is intuitive, but there is no documentation or tutorial, so the reader must already be familiar with the mathematics. Some textbooks on 1D dynamic systems are suggested on his website.
by mathematician J D Meiss.
Cycle Explorer
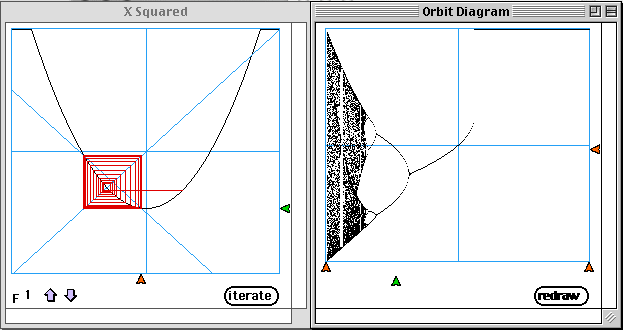
- Cycle Explorer is a simple program that draws orbit maps of the equation f[x]:=x^2+c.
- Author is Jim Burgess.
http://www.efn.org/~jcburg/software.shtml
Mac OS 9 (2003-10)
ABC Map
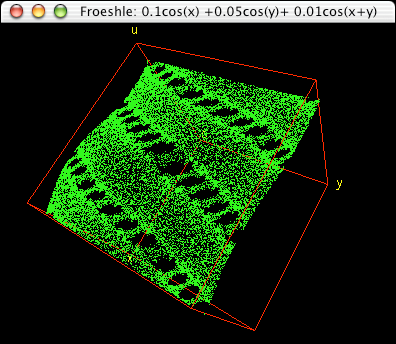
ABC Map “abc, iterate a 3D volume preserving system”. It plots orbit maps of what seems various 3D formulas of significance. I don't quite understand the math here. However, this program is wonderful in that it is like a screensaver with mesmeric images. Dots appears in a 3D box, and these dots fluctuate seemingly ramdomly that forms very distinct patterns. It's like watching statics on TV, but the statics form unpredicable patterns constantly. One can rotate the box. It is a fantastic program even if one knows nothing about the math. The equation it plots has these names: Froeshle, Arnold, ABC, Integrable, Adriana, and others. I hope the author writes a minimum amount of tutorial to benefit the masses.
by mathematician J D Meiss
http://amath.colorado.edu/faculty/jdm/abc.html macOS (2003-10)
Icon Maker
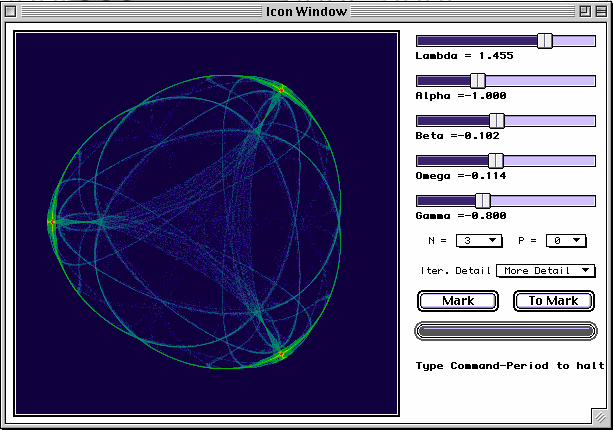
Icon Maker is a simple program that draws orbit maps of the equation
f[z]:=z*(λ + α*z*conjugate[z]+β*Real[z^n]+ω*i)+γ*Conjugate[z]^(n-1)
and other variants. The program is based on ideas in the book Symmetry in Chaos by M Field, M Golubitsky, 1992. This is a wonderful, easy to use, and beautiful program. Author is Jim Burgess.
http://www.efn.org/~jcburg/software.shtml
Mac OS 9 (2003-10)