Sylvester-Gallai Theorem
This is parts of a learning notes from book Real Projective Plane , by H S M Coxeter (1907 to 2003). (Buy at amazon)
Theorem: Sylvester-Gallai theorem
The following result, which plays a useful role in the theory of “harmonic separation”, is particularly interesting because, after its enunciation by Sylvester in 1893, it remained unproved for about forty years. Then T Gallai proved it by an ingenious argument using parallel lines. The projective proof given here is due to R Steibnerg.
Theorem: If n given points are not all on one line, there exists a line containing exactly two of them.
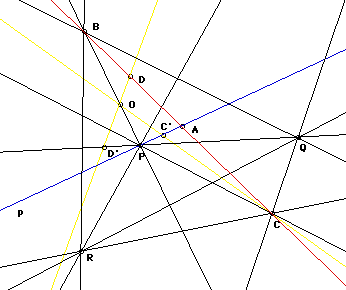
Proof:
Suppose, if possible, that every join of two of the n
points contains a third. Since the points are not all collinear, they
must include three forming a triangle PQR. Let p be a line through P
that contains no other point of the set. All the joins of pairs of the
n points meet p in a certain set of at least two points: P itself, one
on QR, and possibly others. These points occur in a certain cyclic
order. Let A be consecutive to P in this order, so that one of the
segments AP is not met by any of the joins. This point A is not one of
the n but lies on a line containing at least three of them, say B, C,
D, so named that AB//CD. Since P and B are two of the n points, their
join must contain a third, say O. Suppose ABCD /\O==APC'D'. Then
AP//C'D'; that is, the joins OC and OD each meet one of the two
segments AP, contrary to our definition of A. Hence, in fact, one of
the joins must contain only two points of the set.
My proof of Sylvester-Gallai theorem.
First, a lemma:
Lemma: Given n distinct points not all on a line. Let every point be connected to every other by a line. It is not possible for all these lines to meet at a point.
Proof:
For n:=3, the lemma is true. In general, if the lemma is false for n points, it must also be false for n-1 points. (We simply remove one point in the set of n points) By induction, the lemma is true for all n.
Proof: (by induction)
(1) It is true for n = 3.
(2) We want to show: If the theorem is true for n, its true for n+1.
So suppose the theorem is true for n. Call the line that contain exactly two points Line[P1,P2]. Now we add P[n+1] to the set. There are two cases:
(2.a) P[n+1] is not on Line[P1,P2].
If so, then Line[P1,P2] is the line that containing exactly two points.
(2.b) P[n+1] is on Line[P1,P2].
If this is the case, then there are two more cases:
(2.b.1) Every line connecting any of P1,P2,…Pn passes through P[n+1], is NOT true. That is, there are at least one line that does not pass through P[n+1]. Then we just connect P[n+1] with points on that line. The new lines formed will be lines containing exactly two points.
(2.b.2) Every line connecting any pair in P1,P2,…Pn passes through P[n+1]. We know P1,P2…Pn are not all collinear, thus this case is not possible by the above lemma. Thus the proof is complete.
On 2010-05-13, phlexicon wrote to me that my proof is incorrect. The red colored line is the problem.
For full detail of this theorem, see: Sylvester-Gallai theorem .