Intro to Real Projective Plane
The following are notes mostly based on the book Real Projective Plane , by H S M Coxeter (1907 to 2003). Buy at amazon These notes are created in 1996 and was intended to be the basis of an introduction to the subject on the web. Due to personal reasons, the work was put to a stop, and about maybe 1/3 complete.
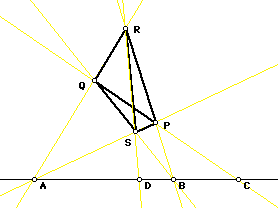
Theorem: Perspective Triangles
If three sides of one triangle are parallel to the three sides of another, the two triangles are similar. That is: Let PQR and P'Q'R' be two triangles. If QR is parallel to Q'R', RP parallel to R'P', and the lines PP', QQ', RR' are concurrent, then PQ is parallel to P'Q'.
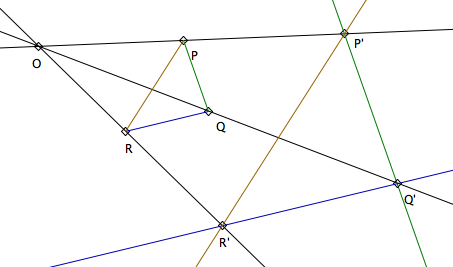
Proof: Euclid Book VI Proposition 2 states: If a straight line be drawn parallel to one of the sides of a triangle, it will cut the sides of the triangle proportionally; and, if the sides of the triangle be cut proportionally, the line joining the points of section will be parallel to the remaining side of the triangle.
Let O be the common point of PP', QQ', RR'. Applying Euclid VI.2 to triangles QOR and Q'OR', ROP and R'OP', we have OQ'/OQ == OR'/OR == OP'/OP. Hence the triangles POQ and P'OQ' are similar, and their corresponding sides PQ and P'Q' are parallel.
Desargues's Two Triangle Theorem
2.2 The Axioms of incidence
- There exist a point and a line that are not incident.
- Every line is incident with at least three distinct points.
- Any two distinct points are incident with just one line.
- Any two lines are incident with at least one point.
- If three lines PP', QQ', RR' are all distinct and incident with one point, then the three points QR*Q'R', RP*R'P', PQ*P'Q' are all incident with one line.
The axioms of incidence can be presented using networks. With this approach, the principle of duality and axiom #5 attains clarity.
Let there be two types of nodes: type P (call point) and type L (called line). We use lowercase letters to label nodes of type L and capital case for nodes of type P.
- There exist a node of type P and a node of type L that are not connected to each other.
- Every L node is connected to at least three P nodes.
- Any two P nodes are connected to one and only one L node.
- Any two L nodes are connected with at least one P node.
- If the following nodes Q',Q,R',R,P',P,b,c,a, and O are connected in such way {{Q',b},{Q,b}, {R',c}, {R,c}, {P',a}, {P,a}, {b,O}, {c,O}, {a,O}}, then there exist nodes p,p',q,q',r,q',A,B,C, and o connected in such way {{p,A},{p',A}, {q,B}, {q',B}, {r,C}, {r',C}, {A,o}, {B,o}, {C,o}} and the nodes p,p',q,q',r,q' connects to nodes Q', Q, R', R, P', P in such a way {{Q',p},{Q,p'},{R',q},{R,q'},{P',r},{P,r'}} and {{Q',r},{Q,r'},{R',p},{R,p'},{P',q},{P,q'}}.
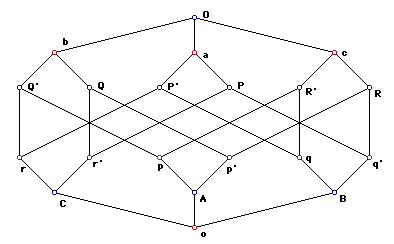
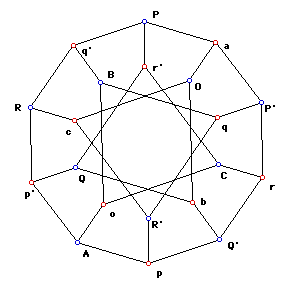
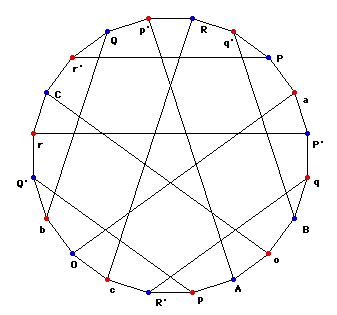
 desarguesGraph.rot
desarguesGraph2.rot)
desarguesGraph.rot
desarguesGraph2.rot)
The graph of axiom 5 (henceforth Desargues's Graph) clearly shows a symmetric relationship between point and line. Desargues's Graph is perfectly symmetric, not just two-fold. We can reposition the graph so any node can serve as one point in a pair analogues to O and o.
We now proceed to prove the dual of the axioms.
Axiom 1 is its own dual.
Now if one plots the graph of axiom 5, its symmetry makes the duality principle obvious. And I think one can prove the dual of theorem of 2 to 4 in one sweep by using axiom 5 with arguments of symmetry. Here's my proof outline.
Axiom 5 is its own dual because it is symmetric.
To prove axiom 2 to 4, we must first show that every node has a structure that of axiom 5. Then axiom 5's symmetry will guarantee that anything that is true of P nodes is also true for L nodes and vice versa.
More specifically, let X or x be a node.
For axiom 2 to 4, just look at the graph of axiom 5. Axiom 5 clearly shows the symmetry of the two type of nodes.
Suppose we are going to prove axiom 2. Pick any L node in axiom 5 that satisfies axiom 2. (all L node in axiom 5 satisfies axiom 2 because otherwise the system will be inconsistent) Now one immediately sees a corresponding P node that is connected to at least L nodes. Since all L node in axiom 5 satisfies axiom 2, so is any P node in axiom 5 will satisfy axiom 2's dual. Now axiom 5 and 2 is true for every non-isolated node, therefore axiom 2's dual inferred from axiom 5 is true for every non-isolated nodes too.
Similar method is used to prove axiom 3 to 4.
2.3 The principle of duality. (p.15)
Proof the duality of the axioms.
1. Axiom one is in its own dual.
2. Every P node is connected to at least three L nodes.
Proof:
Suppose we have a point P1, we'll need to prove that there are at least three lines that is connected to P1.
- By Axiom 3, there must exist a point P2 and line l1 such that {{P1,l1},{P2,l1}}.
- By Axiom 2, l1 must be connected to another point, say P3. So we have {{P1,l1},{P2,l1},{P3,l1}}.
- By Axiom 4, there must be a line l2, together with l1, both connected to a point. This point may be either of P1, P2, P3 or some new point P4. Thus we have four possible cases. The case of P2, P3 are symmetric so we can just consider three cases. The three possible graph we have now is then:
- case 1: {{P1,l1},{P2,l1},{P3,l1}, {P1,l2}}.
- case 2: {{P1,l1},{P2,l1},{P3,l1}, {P2,l2}}.
- case 3: {{P1,l1},{P2,l1},{P3,l1}, {P4,l1}, {P4,l2}}.
Let's work with case 3 first.
By Axiom 2, l2 must be connected to at least two more points. Either one of these points cannot be any of P1, P2, or P3, otherwise Axiom 3 will be violated. So l2 is connect to two new points P5, P6. We have now {{P1,l1},{P2,l1},{P3,l1},{P4,l1}, {P4,l2},{P5,l2},{P6,l2}}.
By Axiom 3, the pair P1,P5 must be connected to a line. Similarly for the pair P1,P6. Therefore, P1 is connected to at least three lines.
Now let's work with case 2. It is similar to case 3. By Axiom 2, l2 must be connected to two other new points P4, P5. By Axiom 3, the pair P1,P4 must be connected to a line, same for P1,P5. Therefore P1 is connected to at least three lines.
Now in case 1, two new points P4, P5 is connected to l2. By Axiom 3 applied to all the point nodes, we find that we need at least four new lines. Any of these lines needs at least one new point, and this new point must be connected to P1 through a line node by Axiom 3. Thus P1 is again connected to at least three lines. ∎
3. Any two P nodes are connected to one and only one L node.
4. Any two L nodes are connected with at least one P node.
5. If the following nodes P,P',Q,Q',R,R',a1,a2,a3, and S are connected in such way {{P,a1},{P',a1}, {Q,a2}, {Q',a2}, {R,a3}, {R',a3}, {a1,S}, {a2,S}, {a3,S}}, then there exist nodes p,p',q,q',r,q',A1,A2,A3, and s connected in such way {{p,A1},{p',A1}, {q,A2}, {q',A2}, {r,A3}, {r',A3}, {A1,s}, {A2,s}, {A3,s}} and the nodes p,p',q,q',r,q' connects to nodes P, P', Q, Q', R, R' in such a way {{P,p},{P',p'},{Q,q},{Q',q'},{R,r},{R',r'}} and {{P,r},{P',r'},{Q,p},{Q',p'},{R,q},{R',q'}}
Quadrilateral and Quadrangle
Harmonic Conjugacy
2.6 Ranges and pencils (p.21)
The points on a line are said to form a range, especially when we regard them as the possible positions of a variable point X (which runs along the line). The dual of a range is a pencil, consisting of the lines through one point: the possible positions of a variable line x (which rotates about the point). The common point of the lines is called the center of the pencil.
We proceed to define a one-to-one correspondence between two ranges. This is a rule for associating every point X of the first range with every point X' of the second, so that there is exactly one X' for each X and exactly one X for each X'. It is usually desirable to think of the correspondence as being directed from X to X', that is, to distinguish between this and the inverse correspondence from X' to X. The two ranges need not be on distinct lines. One trivial case, which must not be ignored, is when X' continually coincides with X; this correspondence is called the identity.
There is a similar definition for a correspondence between two pencils or between a pencil and a range. The simplest correspondence of the latter type occurs when we take the section of the pencil by a fixed line o, so that each line x of the pencil is associated with the point X = o*x of the corresponding range, as in Fig.2.6A. The inverse correspondence occurs when we project a range from a fixed point O so that each point X of the range is associated with the line x = OX of the corresponding pencil. The existence of these simple correspondences is one of the basic reasons for the efficacy of projective geometry.
In affine (or Euclidean) geometry, the line p (through O) parallel to o would be exceptional, for it would have no corresponding point on o; but when we have extended the affine plane to the projective plane, the corresponding point P is just the point at infinity on o. The line x through O, rotating continuously, determines on o the point X, which runs along to the right, say, until x is parallel to o, then immediately reappears far away on the left and continues running to the right. In affine geometry the point X makes an infinite jump; but in projective geometry its motion, through the single point at infinity, is continuous.
2.7 Perspectivity. (p.21)
Apart from the identity, the simplest correspondence between two ranges is that which occurs when we compare the sections of a pencil by two distinct lines o and o', as in Fig.2.7A. The relation between X on o and X' on o' is such that the line XX' passes through a fixed point O, and we call the correspondence a prespectivity from O, writing
X =/\O= x', or simply X =/\= X'.
Dually (Fig.2.7B) a perspectivity from a line o occurs when the relation between two pencils is such that the point of intersection x.x' lies on a fixed line o; then we write
x =/\o= x', or x=/\=x'.
The following important theorems illustrate the way this notation may be used.
Theorem
It is possible, by a sequence of three perspectivities, to interchange pairs among any four collinear points.
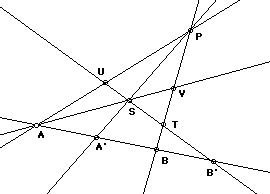
Theorem
It is possible, by a sequence of not more than three perspectivities, to relate any three distinct collinear points to any other three distinct collinear points.
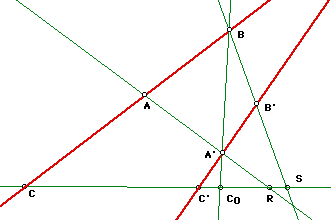
Proof:
If the two triads, ABC and A'B'C' are on distinct lines, let R,S,C0 denote the points where the respective lines AA', BB', BA' meet CC'. Then ABC and A'B'C' are related by the sequence of two perspectivities
ABC =/\R= A'BC0 =/\S= A'B'C'.
Xah's note: this will work for any collinear ABC and A'B'C', regardless of order. Look at the way R is defined, ABC =/\R= A'BC0 will always be true. Similarly for S of A'BC0 =/\S= A'B'C'. Therefore the order of ABC or A'B'C' doesn't matter. And I think we can also reach the conclusion by looking at the cyclic order property on point on a line.
If A and A' coincide, we merely use the perspectivity from S. If the two triads are on one line, we use a quite arbitrary perspectivity ABC =/\= A1B1C1 to obtain a triad on another line and then relate A1B1C1 to A'B'C' by the above construction.
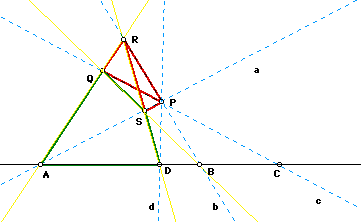
We proceed to show that harmonic sets remain harmonic after any number of perspectives. As a first step we shall prove
Theorem
Any section of a harmonic set of lines is a harmonic set of points, and a harmonic set of points is projected from any point by a harmonic set of lines. Remark: This theorem is in two dual parts, and thus it will suffice to prove the latter part: If A,B,C,D are joined to a point P (outside their line) by lines a,b,c,d and if H(AB,CD), then H(ab,cd).
Proof:
Let P be used as a vertex of the triangle PQR in constructing D from A,B,C. Then the quadrilateral AD,DS,SQ,QA has two opposite vertices on AS=a, two others on BR=b, one vertex Q on c, and one vertex D on d. Hence H(ab,cd)
Combining the above, we conclude that
Theorem
Perspectivities preserve the harmonic relation: If ABCD =/\= A'B'C'D' and H(AB,CD), then H(A'B',C'D')
Our definition for harmonic conjugacy involves A and B symmetrically and likewise C and D. Hence
Theorem
H(AB,CD), H(AB,DC), H(BA,DC), H(BA,CD) are all equivalent.
Chapter 3: Order and Continuity
- 3.1 The axioms of order.
- 3.11 There exists a line containing four distinct points.
- 3.12 If AB//CD, then A, B, C, D are four distinct collinear points.
- 3.13 If AB//CD, then AB//DC.
- 3.14 If A, B, C, D are four distinct collinear points, at least one of the three relations BC//AD, CA//BD, AB//CD must hold.
- 3.15 If AB//CD and AC//BE, then AB//DE.
- 3.16 If AB//CD and ABCD/\A'B'C'D', then A'B'//C'D'.
We need one more axiom on continuity.
Xah's note: Question: why axiom 3.14 so? We can get insight by taking a pair of things out of four things, and there are only three distinct choices. More verbosely, say we have four points A,B,C,D on a circle (their order not specified), the question is how many possible pairs of separation? Since any two pairs separates the other two pair, it is then equivalent to ask how many distinct pairs may be picked? The answer is three, namely, {A,B}, {B,C}, {C,A}. When we picked {A,B}, the other two point is {C,D}, likewise {B,C} leaves {A,D} and {A,C} leaves {B,D}. Thus we have AB//CD, BC//AD, CA//BD as in the axiom.
The first five of these six axioms express the obvious properties of points arranged around a circle. Accordingly, we often find it convenient to use a circular diagram when dealing with points on a single line. (e.g. Fig. 3.1A) illustrates 3.15. (this does not mean that we imagine the line to be somewhow 'bent', but it emphasizes the important fact that th line is 'closed'.)
In contrast to these five one-dimensional axioms, 3.16 is essentially two-dimensional, relating order on one line to order on another. It enables us to derive the dual statement concerning the relation ab//cd for concurrent lines.
3.3
Sylvester-Gallai Theorem
…
Theorem
The three diagonal points of a quadrangle are never collinear.
Proof:
A quadrangle with collinear diagonal points would constitute a configuration of seven points and seven lines such that every two of the points are joined by a line containing a third. By 3.31 with n == 7, this is impossible.
… Considering the quadrangle ABPQ of fig.2.5 A, we deduce
Theorem
If A,B,C are all distinct, H(AB,CD) implies D != C.
Proof: (by Xah)
Given H(AB,CD), by definition there is a quadrangle PQRS such that RQ*PS==A, PR*QS==B, QP*AB==C and RS*AB==D. So we have R,S,D collinear. Also, ABPQ forms a quadrangle with S,C,R as its diagonal points. By 3.32, we know that R,S,C cannot be collinear. If D==C, then R,S,C is collinear because R,S,D is collinear. Thus we have a contraction, therefore D != C.
In other words, if A,B,C are distinct and H(AB,CD) then A,B,C,D are all distinct so that, by 3.14 and 3.17, exactly one of the three relations BC//AD, AC//BD, AB//CD must hold. Since the relation H(AB,CD) is equivalent to H(BA,CD), neither of the relations BC//AD, AC//BD could hold without the other. Hence, among the three relations, the one that holds can only be the third. Thus we have
Theorem
If A,B,C are all distinct, H(AB,CD) implies AB//CD.
Combining 3.33
3.34
Theorem
If A,B,C are all distinct, H(AB,CD) implies AB//CD.
Combining 3.33 with 2.72 and 2.82, we deduce that
Xah's Note: I don't following 3.35. But this could be proved by finding a quadrangle.
3.35
Theorem
H(AB,CD) implies H(CD,AB), and the four equivalent relation 2.83 can be extended to eight.
3.4 Ordered correspondence.
All ordered correspondence is sense preserving. That is to say, if S(ABC) == S(DEF), then S(A'B'C) == S(D'E'F').
Now, there are two kind of sense preserving: Direct and Opposite. the function 1/#& is opposite and has two invariant points -1, 1. The function -1/#& is direct and has one invariant point the Infinity.
Question: What characterize direct and opposite ordered correspondence?
This questions stems from studying projective geometry, but I think it is a elementary idea in topology, which I have not studied. I think many of you who had elementary topology can also help me. Here is my problem in more detail, first in terminology of projective geometry, then in non-proj. geom. terms.
H.S.M. Coxeter says: Any ordered correspondence preserves the distinction of sense, i.e. the relation S(ABC) == S(DEF) implies S(A'B'C') == S(D'E'F'); but in the case of a correspondence between superposed ranges (on one line) the question arises as to whether the sense ABC agrees or disagrees with the sense A'B'C'. We call such a correspondence _direct_ or _opposite_ according as S(ABC) == S(A'B'C') or S(ABC) != S(A'B'C').
What I don't understand is how could one determine whether S(ABC) == S(A'B'C')? If the mapping is on superposed ranges as in Coxter's text, then I understand the equation S(ABC)==S(A'B'C') is defined and can be evaluated because all the points A,B,C,A',B',C' are in the same space. But, in general, when one maps one space to another, one usually consider the two spaces separate (viz. domain and range), so how can the sense of two spaces be compared? We can simply "flip" one or the other space to get a different sense without changing the mapping.
Here is my problem in non-proj.geom. terms. We are mapping two real-lines by a one-to-one function f:R^1→R^1.
We are making an ordered one-to-one correspondence of two point-ranges (range = points on a line). It is ordered because image of points A,B,C will also be in that order.
The mapping is called sense preserving if point A,B,C are mapped to point
Insight: Sense is not an intrinsic element in the real projective line. More generally, sense is not an intrinsic element in any space. Example, we could have a 3D coordinate system with points {x,y,z}, but one may have what they call as right-handed axis system, and we can also have a left-handed system. The two system represents the SAME space. In other words, two isomorphic space may have different sense. This analogy can be carried down to mirror images of the plane, or directions on a line. Now suppose we have two ordered sets {1,2,3} and {3,2,1}. The two sets are identical because their elements are identical and the definition for cyclic ordering of their elements is identical: 1<2, 2<3, 3<1, but yet they have different sense.
More corrected insight: Let's limit our discussion to 1D line, so we don't necessarily make wrong statements about other sets or spaces. If our set is an ordered set (including cyclic ordered), then sense IS an intrinsic element of the set. Because the set is ordered, thus it has (two) directions, and thus we have senses (which is a noun that describe the characteristic of having directions). The word sense-preserving and sense-reversing is only used to describe a characteristic of a FUNCTION that maps the SAME SET TO ITSELF. Sense-preserving and sense-reversing are not defined for functions whose domain and range are not identical (as far as I know). Any function that is order preserving (or perhaps equivalent to saying it's continuous) whose domain and range is an ordered set must be either sense-preserving or sense-reversing. (for other spaces involving points or higher dimension, the direction may be more than two…but we are not going to get confused or guess around)
3.41
Theorem: The correspondence between the points of a range and their harmonic conjugates with respect to two fixed points M and N is an opposite correspondence with invariant points M and N.
Xah's Note: Given H(MN,XX'), there exist a quadrangle P,Q,R,S such and such by the definition of Harmonic sets. We merely have to verify that MNX =/\Q= RNP =/\M= QNS =/\R= MNX' to prove that the correspondence is ordered.
Proof:
Since a perspectivity preserves order, so does the resultant or product of any sequence of perspectivities. To prove that the correspondence between harmonic conjugates with respect to M and N is ordered, we exhibit it as the product of three perspectivities with centers Q, M, R, in the notation of Fig.3.4A. Here Q and R are any fixed points collinear with M. A variable point X on the line MN determines
P==NR*QX, S==MP*NQ, X'==MN*RS,
and we have
MNX =/\Q= RNP =/\M= QNS =/\R= MNX'.
Thus the correspondence X->X' is ordered and has M and N as invariant points. Finally, it is opposite since S(MNX) != S(MNX') by 3.22 and 3.34.
Theorem
Two pairs of harmonic conjugates with respect to M and N cannot separate each other.
Proof: Suppose that H(MN,AB) and H(MN,CD). Then A,B,C are three positions of X in the above correspondence, and the respective positions of X' are B,A,D. Since the correspondence is opposite, we have S(ABC) != S(BAD), that is S(ABC) == S(ABD) By 3.22 this means that A and B do not separate C and D. Xah's Note: I need to develop theorems about Senses solely from a definition that AB//CD means S(ABC) != S(ABD).
Theorem
When H(MX,NX'), where M and N are fixed, X->X' is a direct correspondence with invariant points M and N.
Proof:
Using three fixed points O,Q,R (outside the line MN) such that H(MQ,OR), we observe that QX meets RX' in a pint S on ON, and
MNX =/\Q= ONS =/\R= MNX'.
In this case S(MNX) == S(MNX'); for otherwise we should have MN//XX', whereas the relation H(MX,NX') implies MX//NX'. Thus the correspondence is direct.
Needs to go over proofs in chapter 2 again. Especially 3.18, 3.21.
Notes on 2.7, page 22, perspectivity. To make a one-to-one correspondence from two ranges o and o'. Let P be the perspective point. Line through P will intersect o and o' to form points X and X'. If o and o' are not parallel. (if the intersection of line o and o' is not at the point at infinity )
To make a one-to-one correspondence from two pencils O and O'. Let p be the perspective line. Point on p will intersect O and O' to form lines x and x'. If O and O' are not parallel. (if the join of line o and o' is not at the point at infinity )
* Paradox on Inversion of circle and lines: (this one is not about projective geometry)
Theorem
curve A is the inversion of curve B if and only if curve B is the inversion of curve A. And we know that lines inverts into circles. We also know circle inverts into circles. What's wrong?
* Paradox on projection of two lines.
In a plane, let there be a point P and two horizontal line r and s below P respectively. Let there be vertical line l passing through P. Let the intersection of l r be R and l s be S. As l rotates counter-clockwise around P, R and S will move to the right. When l is horizontal, it is said that R and S have move to the point at infinity. Now when R and S move to the right, observe that S moves increasingly faster then R. The distance between R and S is approaching infinity. How then can we say that when l reaches the horizontal position R and S meet at the point at infinity, and the distance between R and S suddenly become zero? Is the neigher of infinity zero?
Answer: Let r be y == -1 and s be y == -2, and P is at the origin. The line l is then y == Tan[t] x, where t goes from Pi/2 to Pi. R and S is then R == {-Cot[t],-1}, S == {-2 Cot[t],-2} and their distance is then Sqrt[Cot[t]^2 +1]. As t approaches Pi, the distance from S to {0,-2} approaches infinity because Limit[-2 Cot[t], t->Pi] == Infinity. we can write Limit[ Sqrt[Cot[t]^2+1], t->Pi]. This we know to be Infinity.
Let there be two parallel line r and s, and a point P above them all lie in the same plane. Let there be a variable line l pass through P. Let the intersection of l and r be R and l and s be S. Suppose there are two parallel line A, x==-1, and line B, x==-2. Let …
Paradox on pencils and ranges: Suppose we are going to make a one-to-one mapping of points on two perpendicular lines o and o'. Let there be a perspective point P not on these two line. At the intersection of o and o', the mapping will be a fixed point, and that's the only one. Now we are going to make a one-to-one mapping of two pencils. We choose a perspective line P, and let points on P that lies on both pencil to make the association. Now by principle of duality
Question: How do one visualize the pencil of a point at infinity? Are they all parallel? If so, how should they be oriented? Perhaps the orientation has no meaning in projective geometry. But then, if we are to make a perspectivity of two ranges (say, two parallel lines) with the perspective point at infinity, the orientation seems to confound the mapping. What happens if the orientation is parallel to them too? Then they all meet at the point of infinity?
Answer: The pencil of a point at infinity are parallel lines. There are many distinct point at infinity. Each one determines an orientation. (I have to think more about this.)
Question: There are many points of at infinity all right, and I suppose they all line on the line at infinity (or vanishing line). By principle of duality, are there then many lines at infinity? and all are pencils of a point at infinity?
Question: Points on a line forms a range, this include a point at infinity. How do you dualize this? Can we then say that lines through a point forms a pencil, including a line at infinity?
To think about: Correspond theories in real projective plane with 3D space. This should give insights to the theories. Such as, are there infinity numbers of lines at infinity?
There are two things, (1) The orientation of the two planes. Are they parallel, intersect, or overlap? (2) The position of the projecting point. Do it lie in outside the plane, on one plane, or on both plane? All together there are the following possibility:
- (1.a) Two plane is parallel. The point lie outside the plane.
- (1.b) Two plane is parallel. The point lie on one plane.
- (1.c) Two plane is parallel. (but the point can not lie on both plane.)
- (2.a) Two plane intersect. The point lie outside the plane.
- (2.b) Two plane intersect. The point lie on one plane.
- (2.c) Two plane intersect. The point lie on both plane.
(1.a) Two plane is parallel. The point lie outside the plane.
Every normal point have a match. Point at infinity seems to match too. Seems to have one fixed point.
(1.b) Two plane is parallel. The point lie on one plane.
Every normal point on B is mapped to P. Point at infinity of B seems to be mapped to the pencil at P on B. Every point on A seem to be mapped to point at infinity of B, except at P there is no mapping. Point at infinity of A seem map to B's point at infinity.
Fixed point seem to be P, and all point of infinity. The symmetry of this systems seems to be weird but still symmetric. Every point on B seems to be sucked into P of A, while every point on A except P is sucked to points of infinity on B.
(2.a) Two plane intersect. The point lie outside the plane.
Perhaps the most easily recognized symmetry. Every point got a match. But on both A and B there is a vanishing line. Point on this line is map to the other plane's point at infinity. There is this peculiarity about this system. That normally we have line through P from all directions. But here, there is one line through P and parallel to both plane that is not needed. So, one point of infinity on both plane got no mapping. Fixed Point is a line.
(2.b) Two plane intersect. The point lie on one plane.
All normal point on B is map to P of A except where A and B intersect is map to a pencil of P. Point at infinity of B is map to P too. Every normal point on A is map to the intersection line on B. Point at infinity of A also seem to map to intersection line of B.
(2.c) Two plane intersect. The point lie on both plane.
Very symmetric. All point not on the intersection, include point at infinity, is map to P.
(3.a) Two plane overlap. The point lie outside the plane.
Very Symmetric. All points are fixed points.
(3.b) Two plane overlap. The point line on both plane.
Very symmetric. A points map to the pencil P, including points at infinity.
Now the analysis. Let the plane be A and B. Let the projecting point be P that may lie in plane A but never on plane B unless A and B overlap.
Other related things to consider: (1) Is there a vanishing line? (2) On one or both plane?
Another question: Can the projecting point lie at infinity? Probably not. We probably don't want to consider that. At this point it doesn't seems compelling an idea. Maybe for higher dimensions projective geometry, yes.
involution: Two pairs of points A,B and A',B' are said to be an involution if there is a special point O, called the center of the involution, on the line containing the four such that OA*OB == OA'*OB'. Likewise, three pairs of points A,B and A', B', A'', B'' are said to be an involution if OA*OB == OA'*OB' == OA''*OB''. The points A and B, A' and B', and A'' and B'' are said to be conjugate points. If there is a point E such that OA*OB == (OE)^2, then E is called a double point. In this case there is a second double point F, and O is the midpoint of EF. The conjugate of O is the point at infinity.
Involution is invariant under projection.
Theorem
Let there be four distinct points D,C,B,E on a circle. The four points form a complete quadrilateral. Let there by a line not passing D,C,B,E. Let the intersection of the line and the circle be M, L, and let the intersection of the line and the three pairs of opposite sides of the quadrilateral by P,Q; I,K; G,H. The points M,L; P,Q; I,K; G,H is an involution.
Harmonic Points: The point A,B,E,F form a harmonic set if A and B are a pair of conjugate points with respect to the double point E and F of an involution. (Alternatively: the cross ratio of a harmonic set is -1.)
Cross Ratio: The cross ratio of four point on a line A,B,C,D is defined to be (AB*CD)/(BC*AD) == (AB/AD)/(BC/CD) == (BA/BC)/(DA/DC). Or more clearly, a fraction whose numerator is the product of two side segments (AB and CD) and the denominator is the product of the middle section BC and the whole length AD.
Suppose distance[A,B] = x, distance[B,C] = y, distance[C,D] = z. cross ratio is than: x z/(y (x+y+z)).
Cross ratio is invariant under projection.
Note: The symmetric representation of Desargues network is shown to me by Ed Pegg Jr, author of http://mathpuzzle.com/ , in his Mathematical Association of America article: http://www.maa.org/editorial/mathgames/mathgames_12_15_03.html