Desargues's Two Triangle Theorem

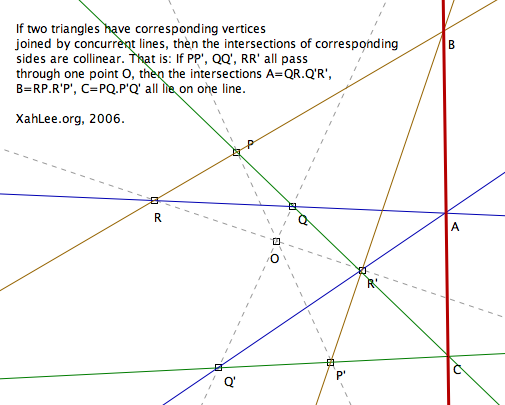
If two triangles have corresponding vertices joined by concurrent lines, then the intersections of corresponding sides are collinear. That is: If PP', QQ', RR' all pass through one point O, then the intersections A=QR.Q'R', B=RP.R'P', C=PQ.P'Q' all lie on one line.

Proof: We need to prove the point C lies on the line AB. Suppose we have two perpendicular planes, the x-y plane and y-z plane. Let there be a projection point P at {-1,0,1}. Let the two triangles PQR, P'Q'R' lie in the y-z plane positioned so that the line AB lies on the vanishing line {x == 0, z == 1}. Since lines whose intersection is on the vanishing line will be projected into parallel lines, therefore by projection onto the x-y plane we obtain two triangles having two pairs of parallel sides. Their remaining sides must be parallel by Theorem 1.51. Since the sides PQ and P'Q' of the original triangles project into these parallel lines, their point of intersections C must lie on the vanishing line AB. ∎

Proof: von Staudt's projective three dimensional proof.
First, we establish that the theorem is true for two triangles PQR and P'Q'R' in distinct planes. In that case, the points A,B,C all lie in the plane PQR and also in the plane P'Q'R', and therefore they all lie on the line of intersection PQR*P'Q'R'.

Take any two points S and S' on a line through O outside the plane of the two given triangles, so that the four lines PP', QQ', RR', SS' all pass through O. Since P, P', S, S' all lie in one plane OPS, the lines PS, P'S' meet in a point P1 (possibly at infinity); similarly, QS meets Q'S' in a point Q1, and RS meets R'S' in a point R1. Applying the theorem on triangles QRS, Q'R'S', which lie in distinct planes, we see that the points of intersection R1 = RS*R'S', Q1 = SQ*S'Q1, A = QR*Q'R' are collinear. Thus A lies on Q1R1; similarly, B on R1P1 and C on P1Q1. Hence the three points A,B,C, lying in the plane P1Q1R1 as well as in the plane PQR, must lie on the line of intersection PQR*P1Q1R1. ∎

Note: von Staudt's proof is difficult to follow, and more difficult to visualize. But understanding will come with persistence. Note that P1,Q1,R1 forms a triangle. Each of A,B,C are collinear with one of its sides, meaning each of A,B,C must lie on one of its side, and thus A,B,C are in the same plane as P1,Q1,R1. Now since A,B,C are on both plane P1,Q1,R1 and P,Q,R, it follows they must be collinear.

Proof:
Take Desargues's theorem of two triangles in distinct planes. Now project them into a plane. Since projection preserve incidence, the figures in the plane satisfies Desargues's theorem in the plane. Now reverse this process to prove Desargues's theorem of two triangles in the plane. (this proofs needs to be clarified)

A special case of Desargues's Theorem is when the corresponding sides are all parallel, we say they met at infinity, and their intersections are collinear on the line at infinity.

Converse of Desargues's Two Triangle Theorem

If two triangle's corresponding sides are collinear, then their corresponding vertices are concurrent.

Proof:
Suppose triangle PQR, and P'Q'R' whose corresponding sides intersect in the three collinear points A,B,C and we wish to prove that the line RR' passes through the point O = PP'*QQ'. This is an immediate consequence of Desargues's two-triangle theorem itself, as applied to the triangle AQQ' and BPP', whose joins of corresponding vertices all pass through C, while their intersections of corresponding sides are O, R', R.

See also: Desargues's Theorem .