Quadrilateral and Quadrangle

Definition: Quadrangle
Four points P, Q, R, S, of which no three are collinear, are the vertices of a complete quadrangle PQRS, of which the six sides are the lines QR, PS, RP, QS, PQ, RS. The intersections of “opposite” sides, namely, A = QR*PS, B = RP*QS, C = PQ*RS, are called diagonal points and are the vertices of the diagonal triangle ABC.

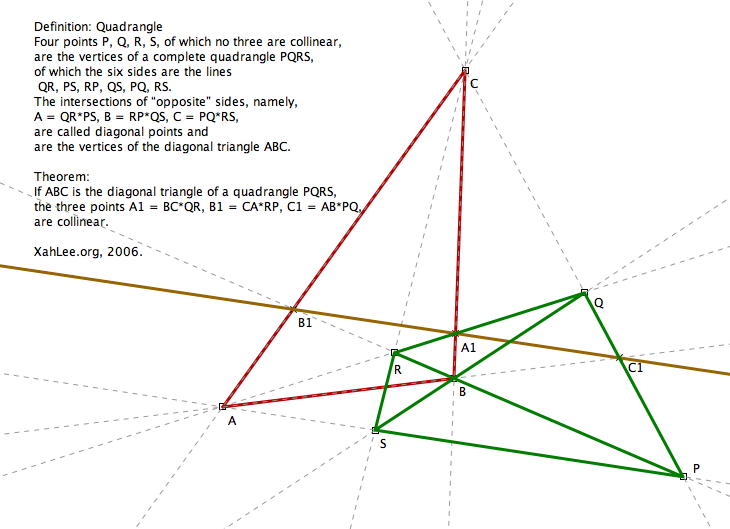
Theorem

If ABC is the diagonal triangle of a quadrangle PQRS, the three points A1 = BC*QR, B1 = CA*RP, C1 = AB*PQ, are collinear.

Proof:
Apply Desargues's theorem to the two triangles ABC and PQR. S is the point of the concurrent center of corresponding vertices of the two triangle.

Xah's note: Now it seems that this theorem breaks the symmetry aspect of the quadrangle. Two questions: (1) In the definition of quadrangle, why FOUR points (P,Q,R,S) are reduced to only THREE points (A,B,C)? Answer: The result is natural. The intersections of lines formed by P,Q,R,S must result three points only. More formally: take all combination of pairs out of {P,Q,R,S}, we have {{P,Q},{Q,R},{R,S},{S,P},{P,R},{Q,S}}. Now any pair of this list will form an intersection. They are thus {P,Q,R,S} and {A,B,C}.

stion 2: Why should S standout as the concurrent point?

Answer: Again, no symmetry is broken. Notice that in the theorem S is also left out in the formation of A1, B1, C1. We can form the theorem by leaving out any of P,Q,R,S, and the one left out will be the concurrent point. The triangle's sides are other collinear lines. Note that they forms a quadrilateral. From this we see the relationship of quadrilateral and quadrangle.

Definition: Quadrilateral

Four lines p,q,r,s, of which no three are concurrent, are the sides of a complete quadrilateral pqrs, of which the six vertices are the points q*r, p*s, r*p, q*s, p*q, r*s. The joins of “opposite” vertices, namely, a = (q*r)+(p*s), b = (r*p)+(q*s), c = (p*q)+(r*s), are called diagonal lines and are the sides of the diagonal triangle.

Xah's Note: Given a quadrangle P,Q,R,S whose sides are the quadrilateral p=SP,q=PQ,r=QR,s=RS, their diagonal triangles will share one common point and one common side. The common point and side depends on the positions of the quadrangle.

Theorem

Given the diagonal triangle and one vertex of a quadrangle, the remanining three vertices may be constructed by incidences.

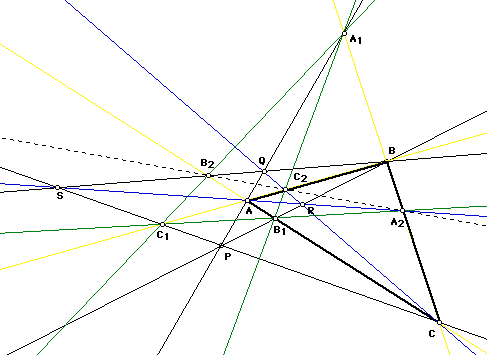
Proof: (by Xah)
Call the vertices of the given triangle A,B,C and the given vertice P, and we are to construct the rest vertices Q,R,S.

Construct lines through P and A, B, C. Three more points will be formed: A1 = (BC)*(PA), B1 = (CA)*(PB),C1 = (AB)*(PC). Triangle A,B,C, and A1, B1, C1 satisfy Desargues's theorem through the point P, thus the intersection of their corresponding sides A2 = (B1C1)*(BC), B2 = (C1A1)*(CA),C2 = (A1B1)*(AB) are collinear.

Among points A1,B1,C1, one of them will intersect one side of the triangle A,B,C. Among points A2,B2,C2, two of them will. Take those that do, then intersection them with opposite vertex. The three lines will be concurrent and the point is R, one point on the quadrangle, the one inside its diagonal triangle. The rest is easy.