Barth Sextic

Barth Sextic is a algebraic surface of degree 6. Its formula is:

b = 0;
phi=GoldenRatio;
ContourPlot3D[
4*(phi^2*x^2 - y^2)*(phi^2*y^2 - z^2)*
    (phi^2*z^2 - x^2) - (1 + 2*phi)*(x^2 + y^2 + z^2 - b^2)^2*b^2,
  {x, -2, 2}, {y, -2, 2}, {z, -2, 2}]

where phi is the golden ratio and b is the parameter. In the above plot, b=1.

It's interesting because it has the maximum of double points for a degree 6 surface. It has 65 double points.

a double point is like the tip of a cone, a point that satisfies all of the following:

f[x,y,z] == 0
D[f[x,y,z],x] == 0
D[f[x,y,z],y] == 0
D[f[x,y,z],z] == 0

D[f[x,y,z],x] means derivative with respect to x.

Barth Sextic is found by Wolf Barth in 1996.

• Wolf Barth, Two projective surfaces with many nodes, admitting the symmetries of the icosahedron, Journal of Algebraic Geometry 5 (1994), 173–186.

The related surface is Barth decic of degree 10 with 345 double points.

Barth Sextic has icosahedral symmetry.

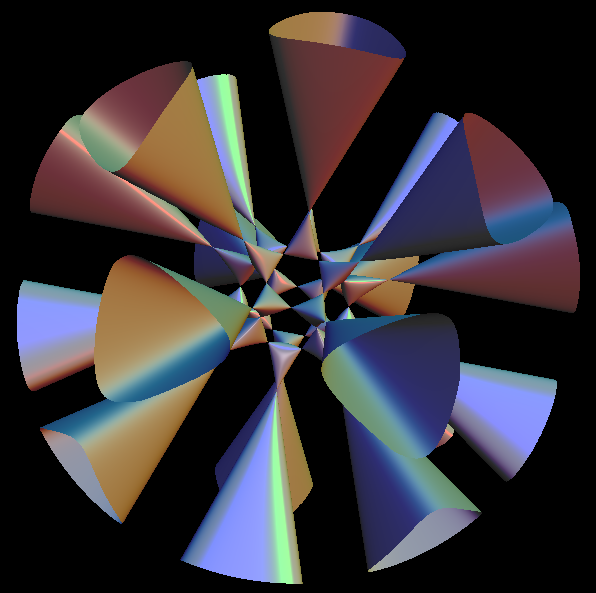
When b is 0, the surface is 6 intersecting planes, arranged in a way like 3 sets of x-crossed planes intersecting from mutually orthogonal directions. In the above image, the cleavages is an artifact of plotting software.

Barth Sextic parameter change, b goes from 0 to 1.

Barth sextic rotated cutaway view 46634 — Barth sextic: A view obtained by applying a rotation involving the w (homogeneous) coordinate in order to make the 15 ordinary double points (the cone-like features) that are located on the plane at infinity visible. The cut is along the (transformed) plane at infinity. [by Abdelaziz Nait Merzouk Apr 21, 2016 at ~~https://plus.google.com/114982179961753756261/posts/B6zWUjNTaVr~~ ]

barth sextic golden — Barth sextic. [by Abdelaziz Nait Merzouk Apr 21, 2016 at ~~https://plus.google.com/114982179961753756261/posts/B6zWUjNTaVr~~ ]

Barth Sextic Mapped to a Unit Sphere

barth sextic mapped to sphere — Barth sextic. The inverse of the mapping: R^3 → R^3 : p → 2 p / ( 1 p²) maps the plane at infinity onto the unit sphere. We also end up with two copies of the euclidean space: One inside the unit sphere and the other outside. In these pictures, the [by Abdelaziz Nait Merzouk Apr 24, 2016 at ~~https://plus.google.com/114982179961753756261/posts/VbbbqdaCbVf~~ ]

barth sextic mapped to sphere cutaway view — Barth sextic. The inverse of the mapping: R^3 → R^3 : p → 2 p / ( 1 p²) maps the plane at infinity onto the unit sphere. We also end up with two copies of the euclidean space: One inside the unit sphere and the other outside. In these pictures, the [by Abdelaziz Nait Merzouk Apr 24, 2016 at ~~https://plus.google.com/114982179961753756261/posts/VbbbqdaCbVf~~ ]

Barth Decic

Reference

[Barth Sextic 2016-04-15 By John Baez. At http://blogs.ams.org/visualinsight/2016/04/15/barth-sextic/ , accessed on 2016-05-02 ]