Costa Surface
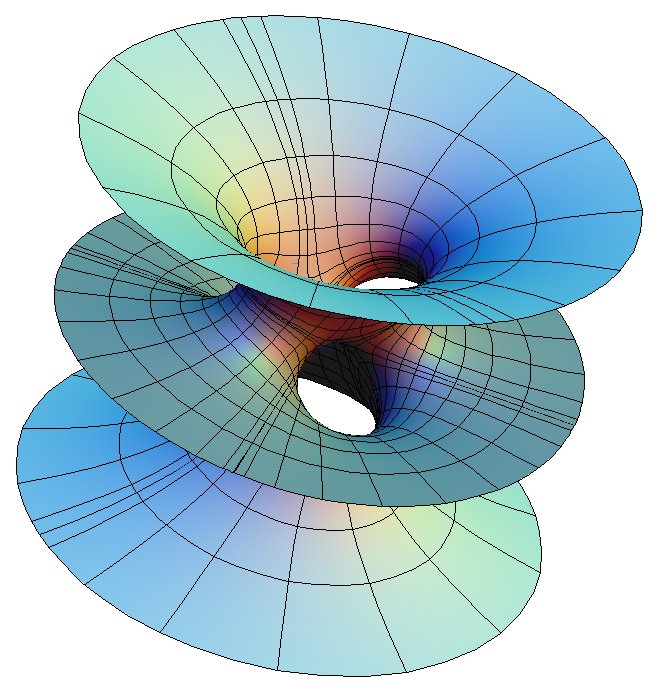
The following explanation are excerpts from 3D-XplorMath's documentation file on this surface, written by Hermann Karcher.
This surface was responsible for the rekindling of interest in minimal surfaces in 1982. It is a minimal EMBEDDING of the 3-punctured square Torus. Its planar symmetry lines cut this surface into four conformal squares and the two straight lines through the saddle are the diagonals of these squares. Because of the emphasis on the symmetries, our formulas are taken from [K2.].
The Gauss map of such a surface is determined by its qualitative properties only up to a multiplicative factor cc which we suggest for the morphing (as in the Chen-Gackstatter case). It closes the period (at cc0) with an intermediate value argument.
After Costa's existence discovery, Hoffman-Meeks proved embeddedness; they also found a deformation family through rectangular tori, where the middle end deforms from a planar one to a catenoid end. They generalized this family to any genus by increasing the dihedral symmetry.