Planar Enneper
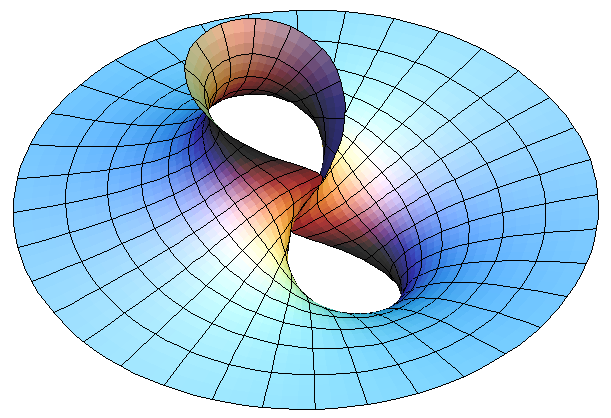
The following explanation are excerpts from 3D-XplorMath's documentation file on this surface, written by Hermann Karcher.
The surfaces Wavy Enneper, Catenoid Enneper, Planar Enneper, and Double Enneper are finite total curvature minimal immersions of the once or twice punctured sphere—shown with standard polar coordinates. These surfaces illustrate how the different types of ends can be combined in a simple way.
The pure Enneper Surfaces (Gauss(z)=z^k ) and the Planar Enneper Surfaces have been re-discovered many times, because the members of the associate family are CONGRUENT surfaces (as can be seen in the interesting associate family morphing!!) and the Weierstrass integrals integrate to polynomial (respectively rational) immersions.
Formulas are taken from: H. Karcher, Construction of minimal surfaces, in “Surveys in Geometry”, Univ. of Tokyo, 1989, and Lecture Notes No. 12, SFB 256, Bonn, 1989, pp. 1—96.
For a discussion of techniques for creating minimal surfaces with various qualitative features by appropriate choices of Weierstrass data, see either [KWH], or pages 192—217 of [DHKW].
- [KWH] H. Karcher, F. Wei, and D. Hoffman, The genus one helicoid, and the minimal surfaces that led to its discovery, in “Global Analysis in Modern Mathematics, A Symposium in Honor of Richard Palais' Sixtieth Birthday”, K. Uhlenbeck Editor, Publish or Perish Press, 1993
- [DHKW] U. Dierkes, S. Hildebrand, A. Kuster, and O. Wohlrab, Minimal Surfaces I, Grundlehren der math. Wiss. v. 295 Springer-Verlag, 1991