Whitney Umbrella

Whitney Umbrella is the surface of this equation: “x^2-y^2*z == 0”. Note that the z-axis is part of the surface.

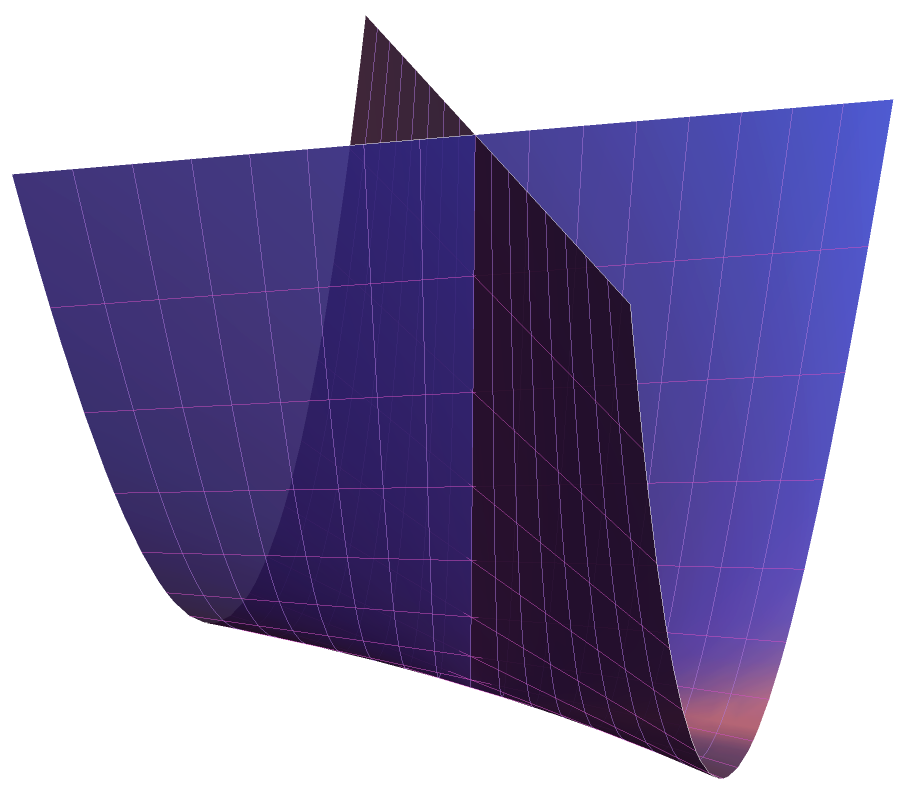
whitney umbrella pHfBR
whitney umbrella 
ParametricPlot3D[{u*v, u, v^2}, {u, -2, 2}, {v, -2, 2},
 BoxRatios -> {1, 1, 1}, Axes -> False, Boxed -> False,
 BoundaryStyle -> {Thin, White}, PlotPoints -> 25,
 MeshStyle -> {RandomColor[], RandomColor[]},
 PlotStyle ->
  Directive[RandomColor[], Opacity[0.9], Specularity[White, 30]]]
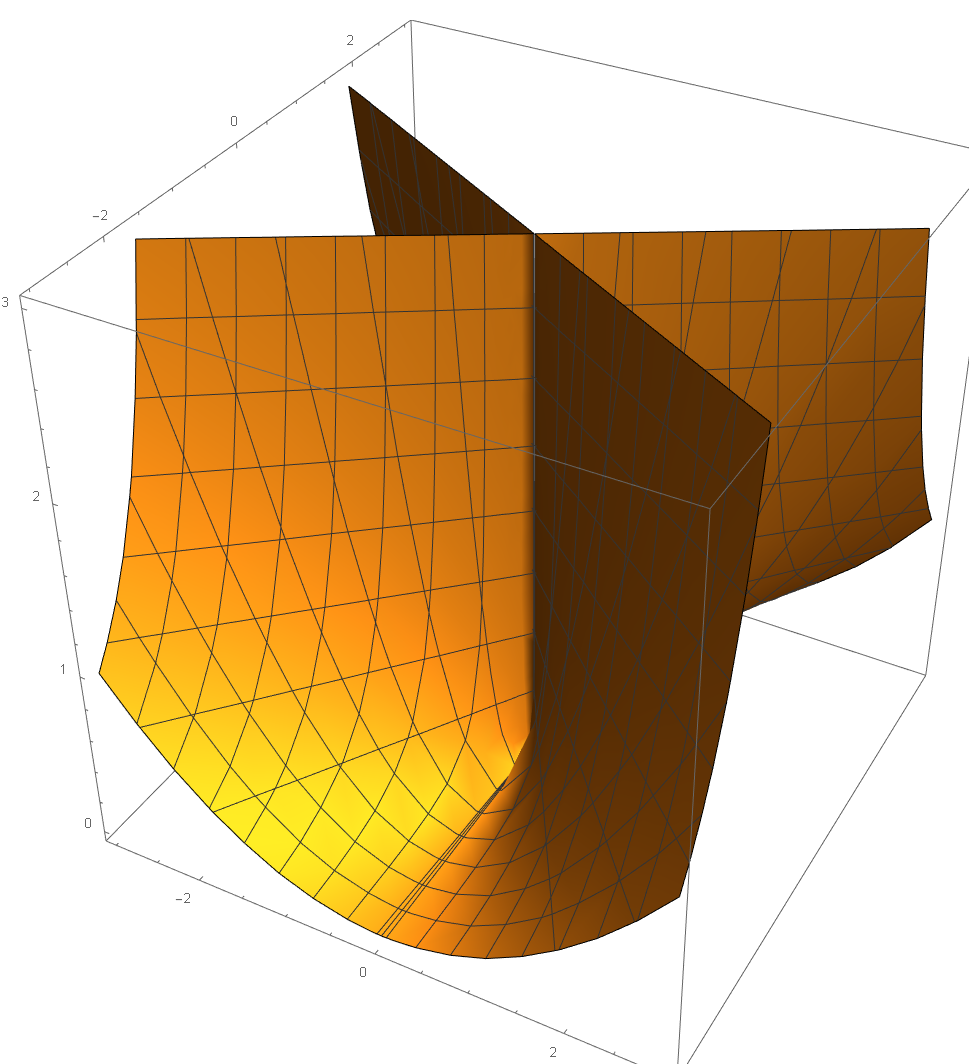
whitney umbrella CQb4d
whitney umbrella 
ContourPlot3D[x^2 - y^2*z == 0, {x, -3, 3}, {y, -3, 3}, {z, -3, 3},
 PlotRange -> All]
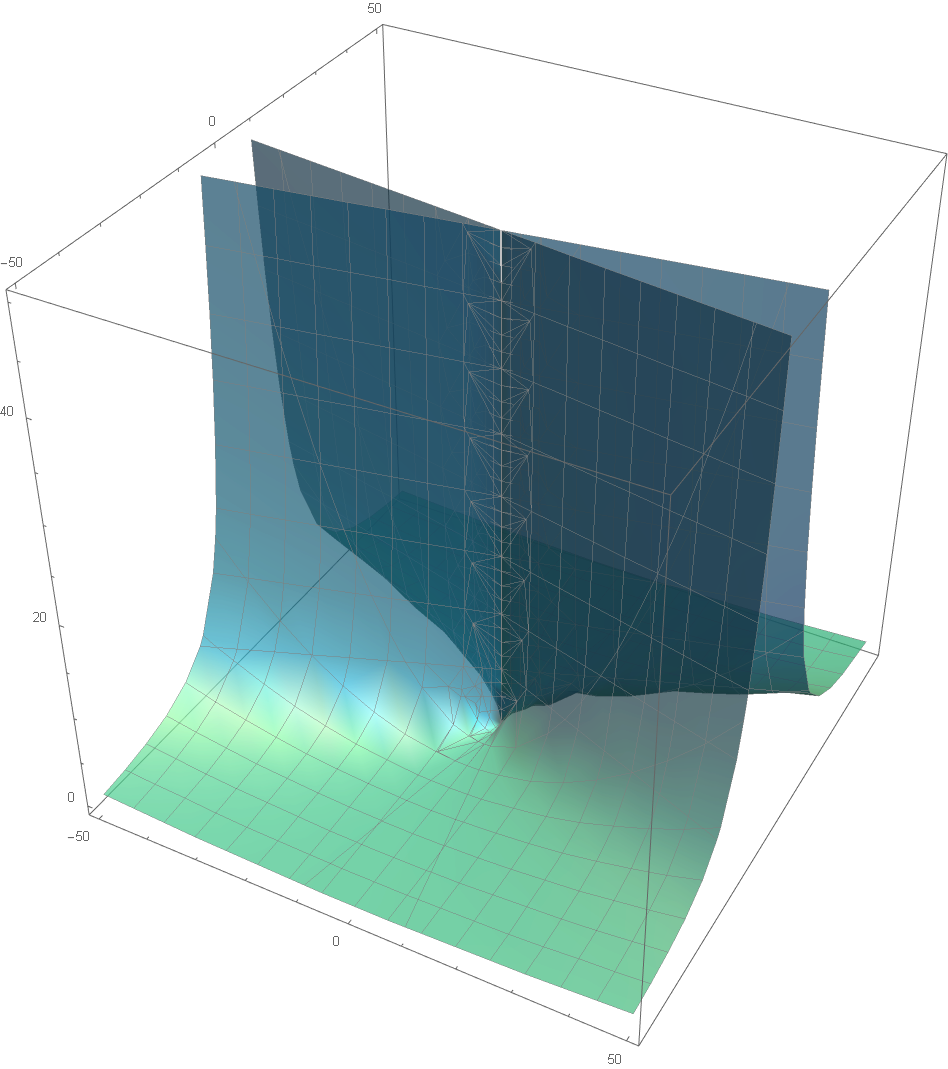
whitney umbrella dxtYH
whitney umbrella 
m = 50;
ContourPlot3D[x^2 - y^2*z == 0, {x, -m, m}, {y, -m, m}, {z, -m, m}, PlotRange -> All, Mesh -> All,
  Boxed -> True, Axes -> True, MeshStyle -> {Gray},
  ContourStyle -> Directive[RandomColor[], Opacity[0.7], Specularity[1, 20]]]
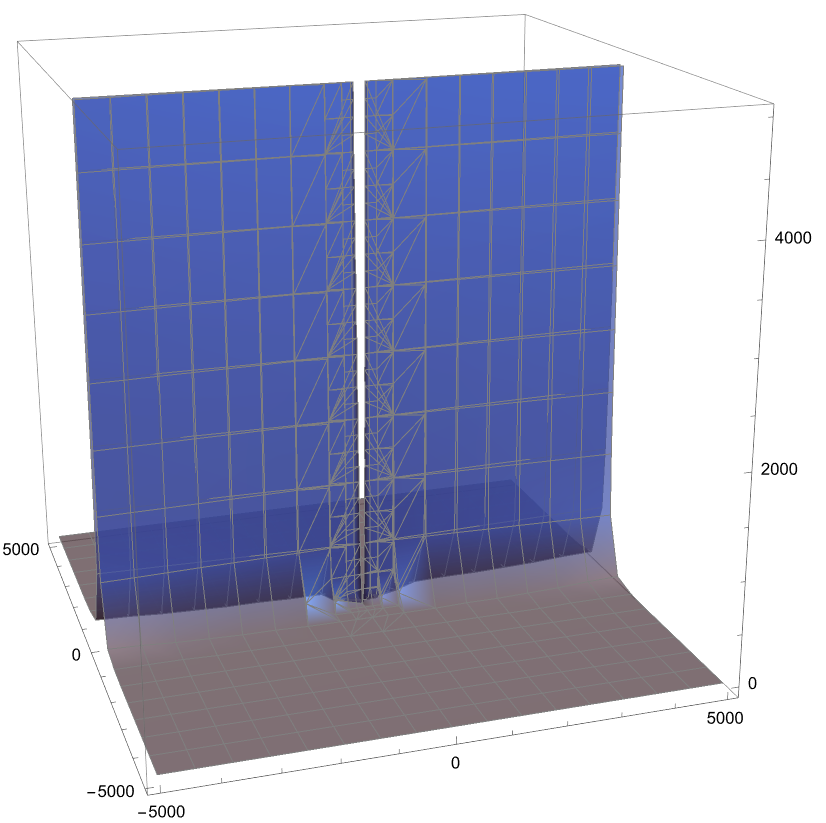
whitney umbrella 5xYfs 
m = 5000;
ContourPlot3D[x^2 - y^2 z == 0, {x, -m, m}, {y, -m, m}, {z, -m, m},
 PlotRange -> All, Mesh -> All, Boxed -> True, Axes -> True,
 MeshStyle -> {Gray},
 ContourStyle ->
  Directive[RandomColor[], Opacity[0.7], Specularity[1, 20]]]