Intro to Mathematica Graphics Format

By Xah Lee. Date: 2006-12-20

A Mathematica graphics format looks like this:

Graphics3D[{
Cuboid[{0, 0, 0}],
Point[{1.5, 1.5,0}],
Polygon[{{2, 2, 1}, {2, 1, 1}, {1, 2, 1}}]
}]

Here's how this code is rendered in Mathematica:

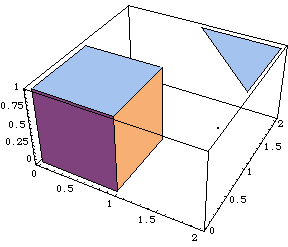
Basic Mathematica Graphics Primitives

The Mathematica graphics format starts with Graphics3D[]. Anything else is enclosed in the square brackets. The first thing inside Graphics3D is a list denoted by curly braces {}. All geometric objects are placed inside this list.

Then, inside this list, each element is a Graphics Primitive, and each are separated by comma. For example, like this: Graphics[{gp1, gp2, gp3, …}]

The following are the graphics primitives you can use.

Point

Point[{x,y,z}] means a point. The x, y, z are the coordinates of the point.

Polygon

The Polygon primitive takes this form: Polygon[{vertex1, vertex2,…}] where the vertex1, vertex2 etc are coordinates for the vertexes of the polygon. Each vertex has the form {x,y,z}, where the x, y, z are numbers that represent a vertex. So, for example, this is a valid polygon:

Polygon[{ {0,0,0},{1,0,0},{0,1,0} }]

It represents a triangle.

There are no limit to the number of vertexes in a Polygon. The polygon can also be non-convex or non-planar. However, non-convex and non-planar polygons usually don't make any sense when rendered. The Polygon graphics primitive represents a filled polygon in space.

Line

The Line primitive has a syntax exactly the same as Polygon. For example, this is a valid line primitive: Line[{ {0,0,0},{1,0,0},{0,1,0} }].

The difference between Line and Polygon is that the latter is filled. For example, Line[{ {0,0,0},{1,0,0},{0,1,0} }] is a triangle rendered as 3 lines, and Polygon[{ {0,0,0},{1,0,0},{0,1,0} }] is a triangle patch.

A surface is built with a set of Polygon, while a wireframe is build with a set of Line.

Cuboid

The Cuboid graphics primitive represents a brick. It has the form Cuboid[{xMin,yMin,zMin}, {xMax,yMax,zMax}], where the points specify the two opposite corners. If the second corner is omitted, then {xMin+1,yMin+1,zMin+1} is assumed.

That's it. Geometric objects in the Mathematica language is very simple. Most of the time, Mathematica 3D graphics will be just a list of Polygons. Mathematica graphics also supports coloring of surfaces, lighting, viewing angle, etc., but as far as geometric modeling is concerned, Cuboid, Point, Line, Polygon is all there it is.

You can use any text editor or programing language to create the text file of Mathematica graphics. To render them, you can use the free tools such as LiveGraphics3D on JavaView.

See:

There are also numerous freely available Mathematica packages that export Mathematica graphics into various formats. For example, AutoCAD DXF and POV-Ray's “.inc” format.

Graphics3D

For many examples of Mathematica graphics rendered in JavaView, see: Minimal Surfaces Gallery .