Geometry: Transformation of the Plane II

By Xah Lee. Date: . Last updated: .

The following are images of transformations in the plane.

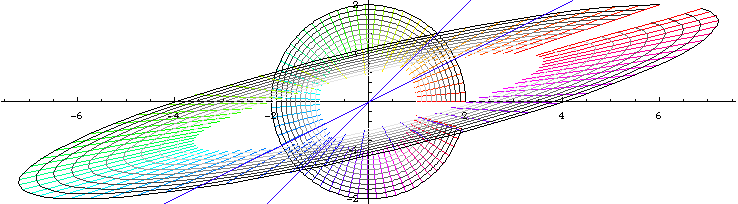
linear transformation
Saturn. The preimage and image of a linear transformation on a polar grid by the matrix {{3,-2},{1,0}}. The matrix has two independent eigenvectors {1,1} and {2,1}, indicated by blue lines. Their significance is that points on those lines will remain on those lines.
bloodyTaiChi.png BM3rC
Bloody Tai-Chi Varing concentric rotation applied to a hexagonal grid. 
Clear[n]; n = N[Pi/3];
Transform2DGraphicsPlot[TriangularGrid[Pi, 49],
   Function[{x,
   y}, ({{Cos[#1*n], -Sin[#1*n]}, {Sin[#1*n], Cos[#1*n]}} & )[
    Norm[{x, y}]] . {x, y}], ResolutionLength -> 0.2,
   AspectRatio -> Automatic]
Varying concentric rotation applied to half of a polar grid.
transformation
Starwave. The Sin[Norm[v]] * 0.4 * Normalize[v] + v applied to a wallpaper design.
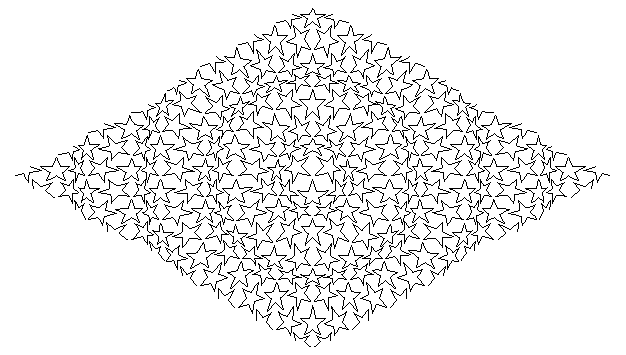
transformation
Stareye. Function[{#1,#2}/(Sqrt[#1^2 +#2^2] + 5)] applied to a wallpaper design of stars. This function is often called fish-eye lens.
transformation
Polar mutate. Function[{#2, Cos[#1*#2]}] applied to a polar grid.

Notation Used

These graphics are generated by my Mathematica packages Transform2DPlot.m and PlaneTiling.m. You can get them at Wolfram: Transform2DPlot Package 📦 and Wolfram: Plane Tiling Package 📦 .

Beautiful geometry gallery