Circle Inversion Gallery

inversionCircleGallery.nb

Nested Inversion of Circles

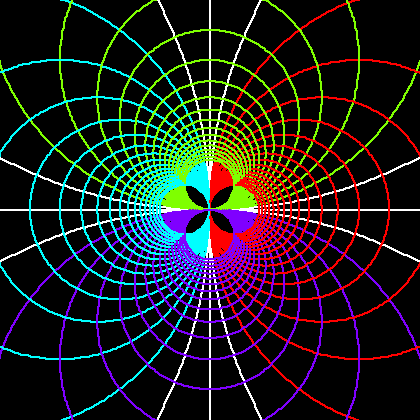
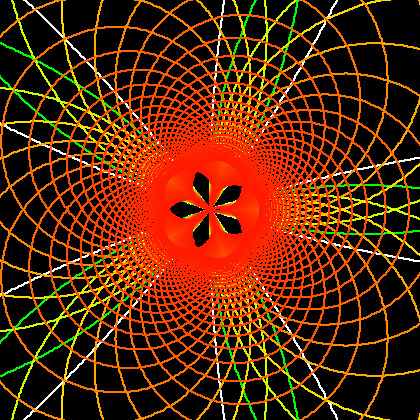
The following images are the geometric inversion of circles. (for math definition, see: Inversion.) Start with set of circles, then invert them with respect to themselves. Take the result and apply inversion with respect to starting circles again. This process can be repeated. Each small graphics show the configuration of the starting (and inverting) circles. Circles retain their color after inversion.

In the first image for example, it starts with seven circles and let's call it generation 0. Invert generation 0 circles with respect to generation 0 circles, we get generation 1. Invert generation 1 with respect to generation 0 we get generation 2… etc. Note that the inversions are always done with respect to generation 0 circles. The image shows the result after 4 inversions.

floral6RingPre
floral6RingPre
hex-floral-ring-2025-08-12
hex-floral-ring-2025-08-12
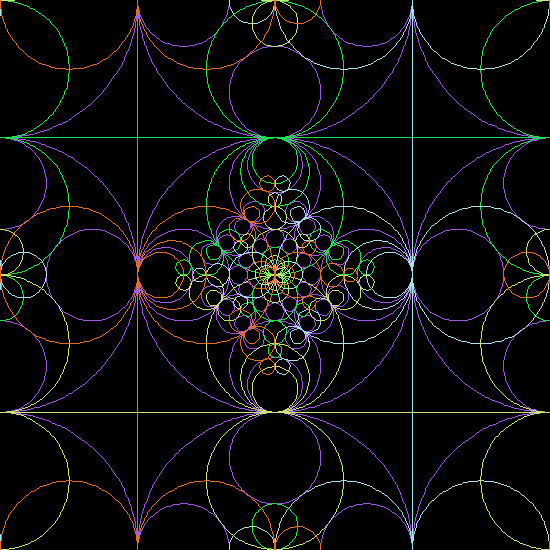
circle inversion
Nested inversion of 6+1 circles. Inverted 4 times. The left is the starting image, the right is the final image. Note that in the starting image, the circles do not touch or overlap. If circles do not overlap, their inverted image will be within the circles. Thus, we get the beautiful effect of nested circles. Nested inversion is analogous to 2 or more mirrors reflecting each other. If a person stands in between those mirrors, she would see a infinite number of reflections.
floral5RingPre
floral5RingPre
circle inversion
Nested inversion of 5+1 circles. Inverted 3 Times. Note that the intersecting circles remains intersecting.
nestedInversion4Pre
nestedInversion4Pre
circle inversion
Nested inversion of 4+1 circles. Inverted 4 Times. Note that there are straight lines in the image. This is because circles tangent to inversion circles will invert to straight lines. Straight lines can be regarded as circles of infinite radius. If we consider line as a special case of circle with infinite radius, then we can say that circles always invert to circles.
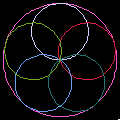
nestedInversion5Pre
nestedInversion5Pre
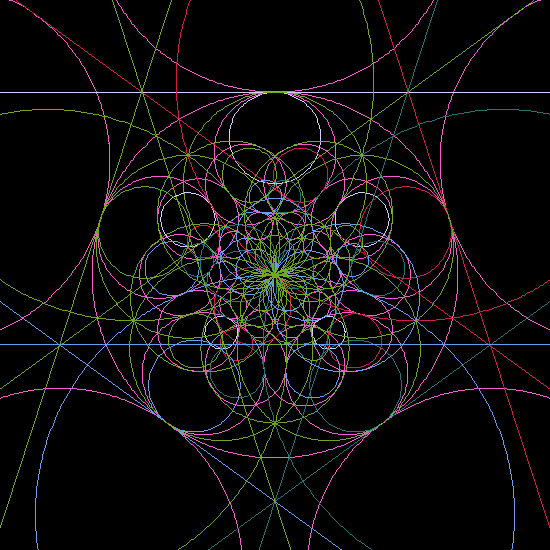
circle inversion
Nested inversion of 5+1 circles. Inverted 2 times.

Inversion of Parallel Lines

The following are inversion of parallel lines with respect to a circle centered on the origin. Color has no significance.

invParallel4Pre
invParallel4Pre
invParallel4
invParallel4
invParallel5Pre
invParallel5Pre
invParallel5
invParallel5
invParallel6Pre
invParallel6Pre
invParallel6
invParallel6

Inversion of a Grid

grid inversion1
grid inversion1
grid inversion2
The before and after image of a inversion transformation applied to a colored grid. (Graphics Code: inversionGrids.nb)

Beautiful geometry gallery