Polynomial (in the works)
Description
Polynomials are functions of the form:
f[x] := a[0]*x^0 + a[1]*x^1 + a[2]*x^2 + … + a[n]*x^n
Or in summation notation:
f[x] := Sum[a[n]*x^n, {0,1,n}]
where a[_] are real numbers and n is a positive integer. For example, the following are polynomials.
- 6
- x^2
- 3 + x^3
- -2*x^5 -4*x^3
Each element in the addition is called a term. For example,
in -2*x^5 -4*x^3, there are two terms: -2*x^5 and -4*x^3. The
constant in each term is called the coefficient of that term. For
example, in the term -2*x^5, -2 is the coefficient. Each term is
associated with a integer called the power or degree of
that term. For example, in -2*x^5, the degree is 5. A polynomial is
associated with a integer called the power or degree of
the polynomial, which is defined to be the max of the degree of
all its terms. For example, the degree of the polynomial -2*x^5
-4x^3 is 5.
The concept of degree of a polynomial is important, because it gives us info about the behavior of the polynomial on the whole. We'll see it when we study the graph of polynomial.
A polynomial can be plotted as to show its properties visually. A polynomial is plotted as the curve “y==f[x]”.
History
The concept of polynomial functions goes way back to perhaps Babylonians times, since for example as simple a need of computing the area of a square y==x^2 is a polynomial, and is needed in buildings and survey, fundamental to core civilization. The Pythagorean theorem x^2+y^2==z^2 is also a polynomial equation, and much basic number theory have been expressed algorithmetically in Greek or pre-Greek era.
The modern concept of polynomial as a function of integer powers and their symbolic manipulation is developed in 1600s and 1700s. Finding solutions of polynomials as ready-made formulas is a spetacular chapter in the history of mathematics, culminating in the birth of Complex Numbers and Group Theory.
Formula
f[x] := Sum[a[n]*x^n, {0,1,n}]
Properties
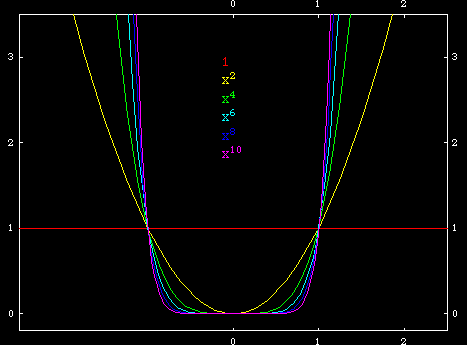
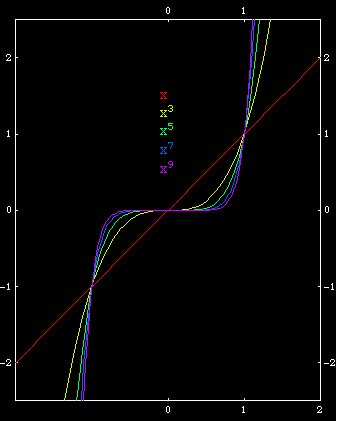
The graph of a polynomial b*x^n looks like a Parabola if n is even. Otherwise, it is s-shaped. These facts can be easily perceived if we look at the behavior of x^n for large values of n. If n is even, x^n is always positive even if x is negative. When n is odd, x^n is negative when x is negative. The coefficient b scales the curve vertically, and if b is negative, it flips the curve along the y-axis.
Given a polynomial f[x] := Sum[a[n]*x^n, {0,1,n}] the overall behavior is its highest term a[n]*x^n…