Parabola
History
Description
Parabola is a member of conic sections, along with hyperbola and ellipse. Parabola can be thought of as a limiting case of ellipse or hyperbola.
Note that parabola is NOT a family of curves. The impression that some parabola are more curved is because we are looking at different scale of the curve. Similarly, part of a large circle appears to be a line may induce us to conclude that there are different shapes of circles.
Like ellipse and hyperbola, there are many ways to define parabola. A common definition defines it as the locus of points P such that the distance from a line (called the directrix) to P is equal to the distance from P to a fixed point F (called the focus). As a conic section, the eccentricity of Parabola is 1.
Needs["PlaneCurveGenerator`"] ListAnimate @ ParabolaGenerator[ {-4.5,2.5}, PlotRange->{{-4.8,5.1},{-1.2,4.8}}, Axes->False, Epilog->{Text["Focus", {0,1},{1.5,-1}], Text["Directrix", {-3,-1}, {0,-1}] } ]
The axis of a parabola is a line perpendicular to its directrix and passing its focus. Vertex of the parabola is the intersection of the parabola and its axis.
Formula
Parametric Equation
ParametricPlot[ {t, 1/4 t^2}, { t, -5, 5} ]
- Vertex at {0,0}
- Focus at {0,1}
the parameter t goes from -Infinity to Infinity
Cartesian Equation
ContourPlot[ y == 1/4 x^2 , {x, -5, 5}, {y, -5, 5}]
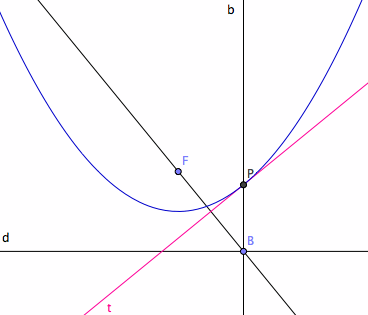
Point and Tangent Construction
Let F be a given point and d be a give line. Let B := Point[d]. Let t := LineBisector[B,F]. Let b := Perpendicular[B,d]. Let P := Intersect[b,t] Since length[segment[B,P]]==length[segment[P,F]], P is a point on parabola. Further, t is the tangent at P.
Invariant under certain Dilation
Parabola have the property that when scaled (streching/shrinking) along a direction parallel or perpendicular to its axis, the curve remain unchanged. (For example, line also have this property, but circle do not. A streched line is still a line, but a streched circle is no longer a circle) When a parabola is streched along the directrix “a” units and along the axis by “b” units, the resulting curve is the original parabola scaled in both direction by “a^2/b”.
Given a parametrization of a parabola {xf[t], yf[t]} with vertex at Origin and focus along the y-axis, its focus is {0, xf[t]^2/(4 yf[t]) }.
Optical Property
A radiant point at the focus will reflect off the parabola into parallel lines. The figure shows three parabolas, two of which share a common focus.
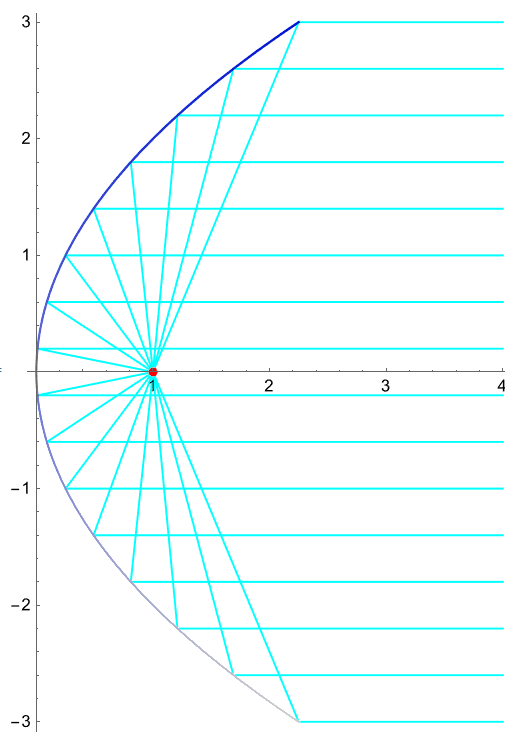
Needs[ "PlaneCurvePlot`" ] PlaneCurvePlot[ {1/4 t^2, t}, {t, -3, 3, .4}, CausticLineLength -> 5, CausticOrigin -> {1, 0}, PlotRange -> All, PlotDot -> False, AspectRatio -> Automatic] xx = Table[PlaneCurvePlot[{1/4 t^2, t}, {t, -3, 3, .2}, CausticLineLength -> 20, CausticOrigin -> {x, 0}, PlotRange -> {{0, 7}, {-1, 1} 3}, PlotDot -> False, AspectRatio -> Automatic], {x, 0.5, 3, 0.1}] ListAnimate@ xx

3 Parabolas Sharing Reflection Rays
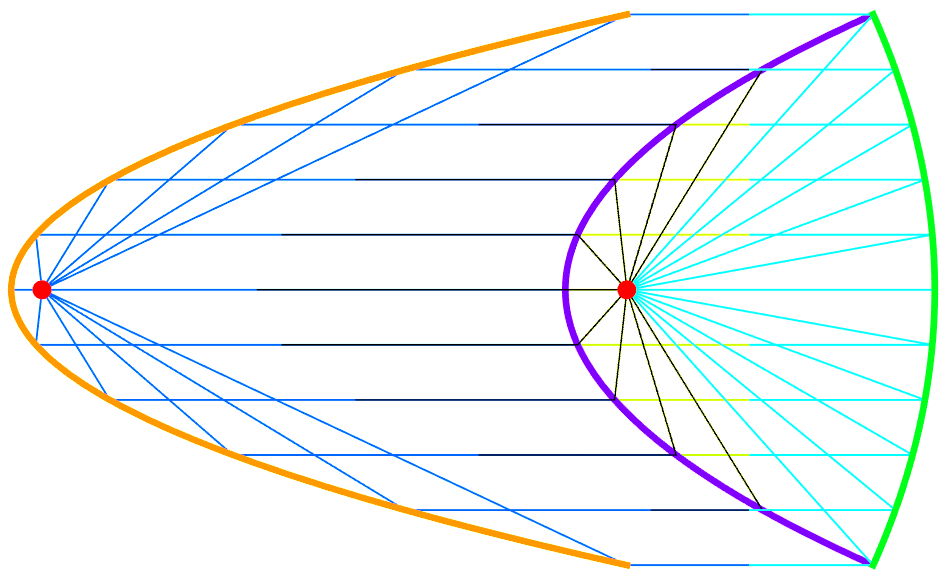
Needs["PlaneCurvePlot`"] Clear[parabola1, parabola2, parabola2LinesGP, parabola3] parabola1 = ParaPlot[ RotationTransform[ -(Pi/2)]@{t, t^2/2} + {-10, 0}, {t, -Sqrt[20], Sqrt[ 20], (2 Sqrt[20])/10}, CausticLineLength -> 13, CausticOrigin -> {-10 + 1/2, 0}, PlotDot -> False, CausticLineStyle -> {{Hue[0.6], Thickness[0.002]}}, CurveColorFunction -> Function[Hue[0.1]], CurveStyle -> {Thickness[0.007]}] parabola2 = ParaPlot[ RotationTransform[ -(Pi/2)] @ {t, 1/4 t^2} + {-1, 0}, {t, -Sqrt[20], Sqrt[ 20]}, Range[-Sqrt[20] + (2 Sqrt[20])/10, Sqrt[20] - (2 Sqrt[20])/10, (2 Sqrt[20])/10.], CausticLineLength -> 4, CausticOrigin -> {0, 0}, PlotDot -> False, CurveColorFunction -> Function[Hue[0.75]], CurveStyle -> {Thickness[0.007]}, CausticLineStyle -> {{Hue[0.2], Thickness[0.002]}} ] parabola2LinesGP = ParaPlot[ RotationTransform[ -(Pi/2)] @ {t, 1/4 t^2} + {-1, 0}, {t, -Sqrt[20], Sqrt[ 20], (2 Sqrt[20])/10}, CausticLineLength -> -6, CausticOrigin -> {0, 0}, PlotDot -> False, PlotCurve -> False ] parabola2LinesGP = Cases[parabola2LinesGP, Line[__], -1] parabola3 = ParaPlot[ RotationTransform[ Pi/2] @ {t, t^2/20} + {5, 0}, {t, -Sqrt[20], Sqrt[20], ( 2 Sqrt[20])/10}, CausticLineLength -> 8, CausticOrigin -> {0, 0}, PlotDot -> False, CurveColorFunction -> Function[Hue[0.35]], CurveStyle -> {Thickness[0.007]}, CausticLineStyle -> {{Hue[0.5, 1, 1], Thickness[0.002]}} ] Show[ { Graphics @ First @ parabola1, Graphics @ First @ parabola2, Graphics @ parabola2LinesGP, Graphics @ First @ parabola3 } ]
Tangents of Probala
Any set of tangents on the parabola will always cut a arbitrary tangent into the same proportion.
- suppose you pick three tangents call them a, b, c.
- Now pick a arbitrary tangent x.
- Tagents a, b, c will cut x into segments with certain proportions.
- Now pick any other tangent x1, it will be cut into the same proportions.
Thus, the envelope of lines with a positive constant sum of intercepts is a segment of parabola.

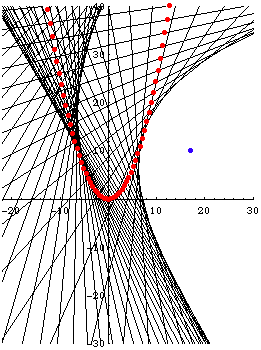
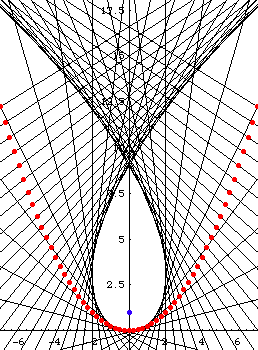
Needs[ "PlaneCurvePlot`" ] PlaneCurvePlot[ {t, 1/4 t^2} , {t,-5,5}, Join[{-2.5, -1, 0.},{1.2, 2., 2.5, 3., 3.8}], TangentLineLength->20, PlotRange->{{-1,1} 4,{-3,4}}, PlotDot->True, Axes->False, CurveStyle->{Thickness[.002]}, CurveColorFunction->Black, TangentLineStyle->Join[ Table[ Red, {3}], Table[ Green, {8}] ] ]
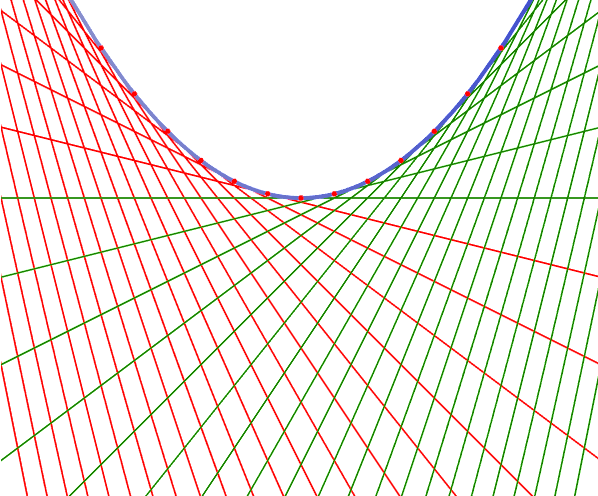
Needs[ "PlaneCurvePlot`" ] PlaneCurvePlot[ {t, 1/4 t^2} , {t,-10,10,.5}, TangentLineLength->100, PlotRange->{{-1,1} 3,{-3,2}} 1.5, PlotDot->True, CurveStyle->{Thickness[.007]}, TangentLineStyle-> Join[ Table[ Hue[0], {20}], Table[ Hue[.3,1,.5], {21}] ], Axes->False ]
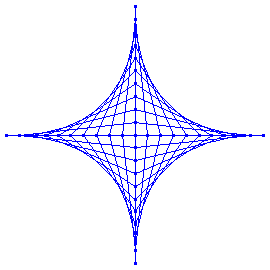
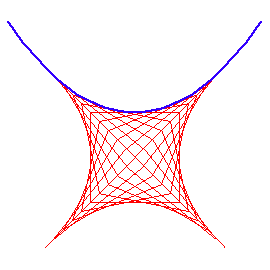
Evolute and Semicubic Parabola
The evolute of a parabola is the semicubic parabola .
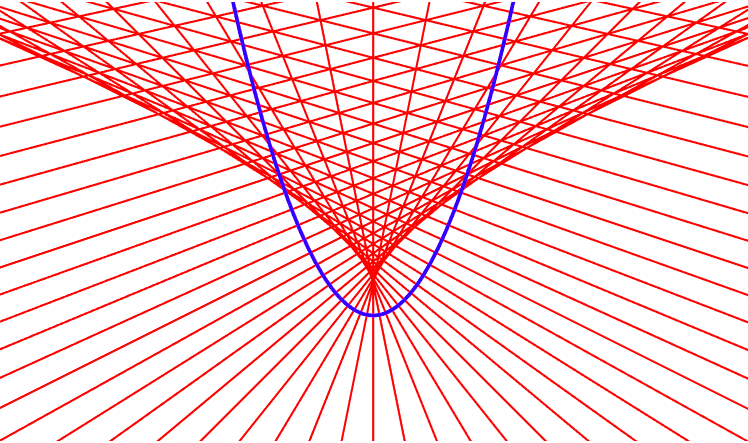
Needs[ "PlaneCurvePlot`" ] ParaPlot[ {t, 1/4 t^2} , {t, -12, 12, 24/60}, NormalLineLength->100, NormalLineStyle->Red, CurveColorFunction->Blue, PlotDot->False, AspectRatio->Automatic, PlotRange->{{-24,24},{-8,20}}, Axes->False ]
Pedal
The pedal of a parabola with respect to its focus is a line

pedal with respect to its vertex is the cissoid of Diocles.

Needs[ "PlaneCurvePlot`" ] PlaneCurvePlot[ {t, 1/4 t^2} , {t, -9, 9, .5}, PedalPoint -> {0, 0}, AspectRatio -> Automatic, PlotRange -> {{-1, 1} 4, {-1.1, 3}}] PlaneCurvePlot[ {t, 1/4 t^2} ,{t, -8, 8, .5}, PedalPoint->{0,1}, PlotCurve->True, PlotDot->True, AspectRatio->Automatic, PlotRange->{{-1, 1} 4,{-1.1,3}} ]
Inversion
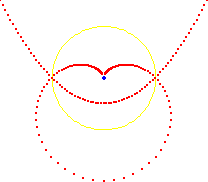
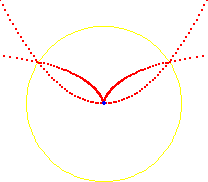
Misc
[string_art_square.mov]
string_art_movie.nb