Math Parametric Equation for Seashell

By Xah Lee. Date: 2006-05-30

The following are some math formulas for seashell, by Mike Willams. (slightly modified)

From: mike@econym.demon.co.uk
Subject: Paramnetric equations of seashells
Date: January 19, 2005 12:35:17 AM PST
To: xah@xahlee.org

I hear that you're interested in parametric equations that approximate spiral seashells. Here are a few that I've made.

They're all based on this parameterisation of the torus

(* a torus *)

R = 1;
R2 = 2;

ParametricPlot3D[ {
R* Cos[u]*(R2+Cos[v]),
R*Sin[u]*(R2+Cos[v]),
R*Sin[v]
},
{u, 0, 6},
{v, 0, 10}
 ]

I then replaced R with R*u/(2*pi) so that the radius of the tube increases linearly as u increases, and replaced sin(u) with sin(N*u) so that the tube spirals round the origin N times. Then I added an offset factor H*(u/2*pi)^P so that the turns of the spiral are offset in the z direction by a distance that varies from 0 to H.

This gives a periwinkle seashell:

periwinkle seashell

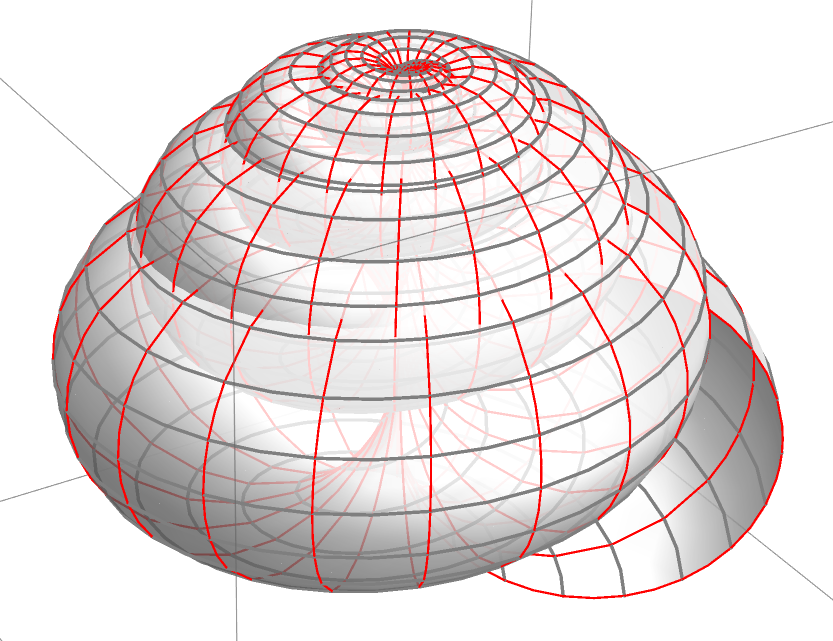
xR = 1; (*radius of tube*)
xturnN = 4.6; (*number of turns*)
xhei = 2; (*height*)
xPower = 2; (*power*)
xf = Function[x, x/(2*Pi)*xR];
ParametricPlot3D[{xf[u]*Cos[xturnN*u]*(1 + Cos[v]),
  xf[u]*Sin[xturnN*u]*(1 + Cos[v]),
  xf[u]*Sin[v] + xhei*(u/(2*Pi))^xPower}, {u, 0, 2   Pi}, {v, 0,
  2   Pi}, PlotRange -> All,
 ColorFunction -> Black,(*MeshShading->{{None},{None}},*)Mesh -> Full,
  MeshStyle -> {{Red, Thickness[0.002]}, {Gray, Thickness[0.003]}},
 PlotStyle -> Directive[White, Opacity[.8], Specularity[1, 9]],
 PlotPoints -> {90, 20}]

top shell

And a top

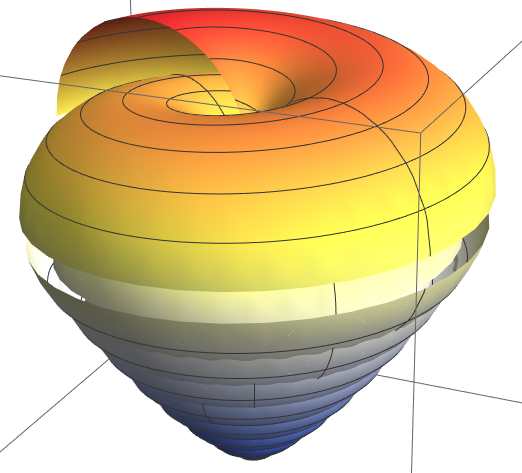
R=1; (* radius of tube *)
cN=7.6; (* number of turns *)
H=2.5; (* height *)
P=1.3; (* power *)

W = Function[ {u}, u/(2*Pi)*R ];

ParametricPlot3D[ {W[u]*Cos[cN*u]*(1+Cos[v]),
W[u]*Sin[cN*u]*(1+Cos[v]),
W[u]*Sin[v] + H*(u/(2*Pi))^P
},
{u,0,7},
{v,0,6},
PlotPoints -> {160,  10}, PlotRange -> All, ColorFunction -> "TemperatureMap"
 ]

cone shell

A cone shell is something like this:

A cone shell is something like this:

R=1;    // radius of tube
N=4.6;  // number of turns
H=0.5;  // height
P=2;    // power

W = u/(2*pi)*R
Fx = W(u)*cos(N*u)*(1+cos(v))
Fy = W(u)*sin(N*u)*(1+cos(v))
Fz = W(u)*sin(v)*1.25 + H*(u/(2*pi))^P +W(u)*cos(v)*1.25

--
Mike Williams
Gentleman of Leisure

	From: 	  private@econym.demon.co.uk
	Subject: 	Parametric equations of seashells
	Date: 	January 20, 2005 9:41:46 PM PST
	To: 	  xah@xahlee.org

You wrote

hi Mike,

Great work!

of your results, i find the wrinkled version of greatest interest. Now it would be great if one can add to the equation periodic spikes, as to make one of those horny ones,

I reckon that this general approach would only be able to place spikes that point in the +-x and +-y directions. This might make something that at first glance resembles a Venus Comb, but the rows of spikes should really point in directions separated by about 120 degrees rather than 90.

For spikes that point in other directions I think you'd need an entirely different approach.

I think the ideal “top” one should have a flat surface, very angular triangular opening, and with a cone shaped hole at the bottom. See * Seashell Gallery: Top Shell

We only have one species of “top” in my country (Britain), the “Toothed Topshell” (Monodonta lineata) and it is quite rounded. A flat sided topshell is more like this:

R=1;    // radius of tube
N=7.6;  // number of turns
H=2.5;  // height
P=1.3;  // power
T=0.8;  // Triangleness of cross section
A=-0.3;  // Angle of tilt of cross section (radians)

W = u/(2*pi)*R

Fx = W(u)*cos(N*u)*(1+cos(v+A)+sin(2*v+A)*T/4)
Fy = W(u)*sin(N*u)*(1+cos(v+A)+sin(2*v+A)*T/4)
Fz = W(u)*(sin(v+A)+cos(2*v+A)*T/4)  + H*(u/(2*pi))^P

Which also gives the possibility of creating something like a turret shell (oddly, my book of British fauna doesn't include these, but there's loads of them on the local beach). I can't quite seem to get the coils to touch each other correctly at the tip.

R=1;    // radius of tube
N=9.6;  // number of turns
H=5.0;  // height
P=1.5;  // power
P1=1.1; // another power
T=0.8;  // Triangleness of cross section
A=0.1;  // Angle of tilt of cross section (radians)
S=1.5;  // Stretch

W = (u/(2*pi)*R)^P1

Fx = W(u)*cos(N*u)*(1+cos(v+A)+sin(2*v+A)*T/4)
Fy = W(u)*sin(N*u)*(1+cos(v+A)+sin(2*v+A)*T/4)
Fz = S*W(u)*(sin(v+A)+cos(2*v+A)*T/4)  + S*H*(u/(2*pi))^P

Whilst trying to get the turret working, I happened to create this by mistake.

R=1;    // radius of tube
N=7.6;  // number of turns
H=2.5;  // height
P=1.3;  // power
T=0.8;  // Triangleness of cross section
A=-0.3; // Angle of tilt of cross section (radians)
S=3.0;  // Stretch

W = u/(2*pi)*R

Fx = W(u)*cos(N*u)*(1+cos(v+A)+sin(2*v+A)*T/4)
Fy = W(u)*sin(N*u)*(1+cos(v+A)+sin(2*v+A)*T/4)
Fz = S*W(u)*(sin(v+A)+cos(2*v+A)*T/4)  + S*H*(u/(2*pi))^P

I should have mentioned (but I guess you've worked it out for yourself) that all these surfaces are designed to be generated with u and v both being in the range 0 to 2*pi.

PS may i forward your results to the curves-surfaces mailing list?

Yes.

Is there an actual mailing list? All I could find at the URL you gave me was one of those horrible Google Groups.

--
Mike Williams
Gentleman of Leisure

spindle shell

R=1;    // radius of tube
N=5.6;  // number of turns
H=4.5;  // height
P=1.4;  // power
L=4;    // Controls spike length
K=9;    // Controls spike sharpness

W = (u/(2*pi)*R)^0.9

Fx = W(u)*cos(N*u)*(1+cos(v))
Fy = W(u)*sin(N*u)*(1+cos(v))
Fz = W(u)*(sin(v)+L*(sin(v/2))^K)  + H*(u/(2*pi))^P

top shell

(* radius of tube *)
tubeRadius = 1;

(* number of turns *)
turns = 7.6;
height = 2.5;
powerP = 1.3;

(* Triangleness of cross section *)
triangleX = 0.8;
(* crossTiltngle of tilt of cross section (radians) *)
crossTilt = -0.3;

ff = Function[x, (x/(2*Pi)* tubeRadius)];

ParametricPlot3D[  {
ff[u]*Cos[turns*u]*(1+Cos[v+crossTilt]+Sin[2*v+crossTilt]*triangleX/4),
ff[u]*Sin[turns*u]*(1+Cos[v+crossTilt]+Sin[2*v+crossTilt]*triangleX/4),
ff[u]*(Sin[v+crossTilt]+Cos[2*v+crossTilt]*triangleX/4)  + height*(u/(2*Pi))^powerP
},
{u,0,3},
{v,0,3},
ColorFunction -> GrayLevel,
PlotPoints -> {90, 10}
]

back to Math of Seashell Shapes