Math of Seashell Shapes

A simple seashell can be modeled using the following parametric formula:
seashell[u_, v_] := {2*(1 - E^(u/(6*Pi)))*Cos[u]* Cos[v/2]^2, 2*(-1 + E^(u/(6*Pi)))*Cos[v/2]^2* Sin[u], 1 - E^(u/(3*Pi)) - Sin[v] + E^(u/(6*Pi))*Sin[v]}; start = 0; end = 2*Pi; gap = 1; shift = 1; uMin = 0; uMax = 6*Pi; xViewPoint = {1.0992, 3.2001, 0.0255}; gra1 = ParametricPlot3D[Evaluate[seashell[u, v]], {u, uMin, uMax}, {v, end - gap + shift, end + shift}, PlotPoints -> {96, 4}, Mesh -> Full, MeshShading -> {{None},{None}}, PlotRange -> All ] gra2 = ParametricPlot3D[Evaluate[seashell[u, v]], {u, uMin, uMax}, {v, start + shift, end - gap + shift}, PlotPoints -> {96, 20}, Mesh -> Full, PlotStyle -> Directive[White, Opacity[.8], Specularity[White, 20]], PlotRange -> All ] Graphics3D[{ gra1[[1]] , gra2[[1]]}, {PlotRange -> All, Boxed -> False, ViewPoint -> xViewPoint}]
wrinkled periwinkle
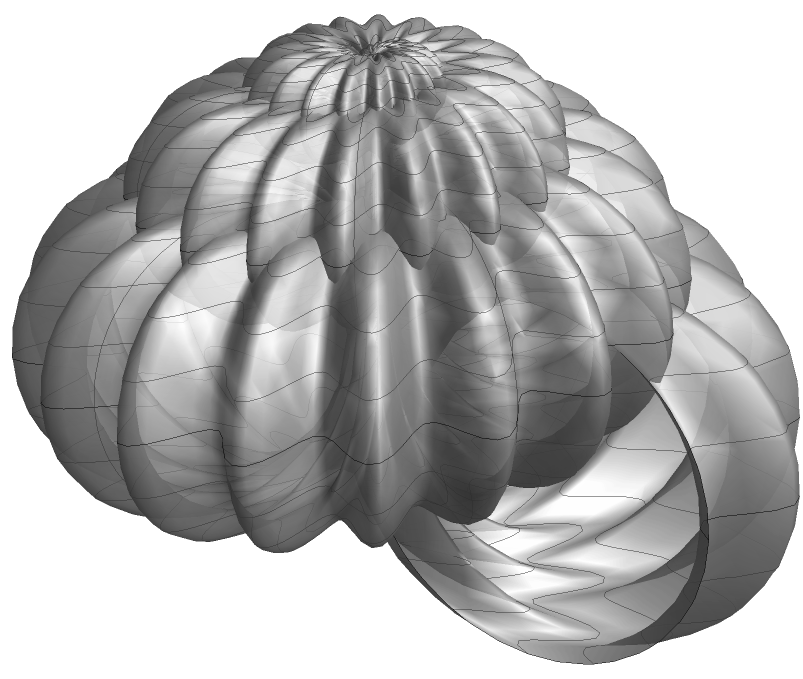
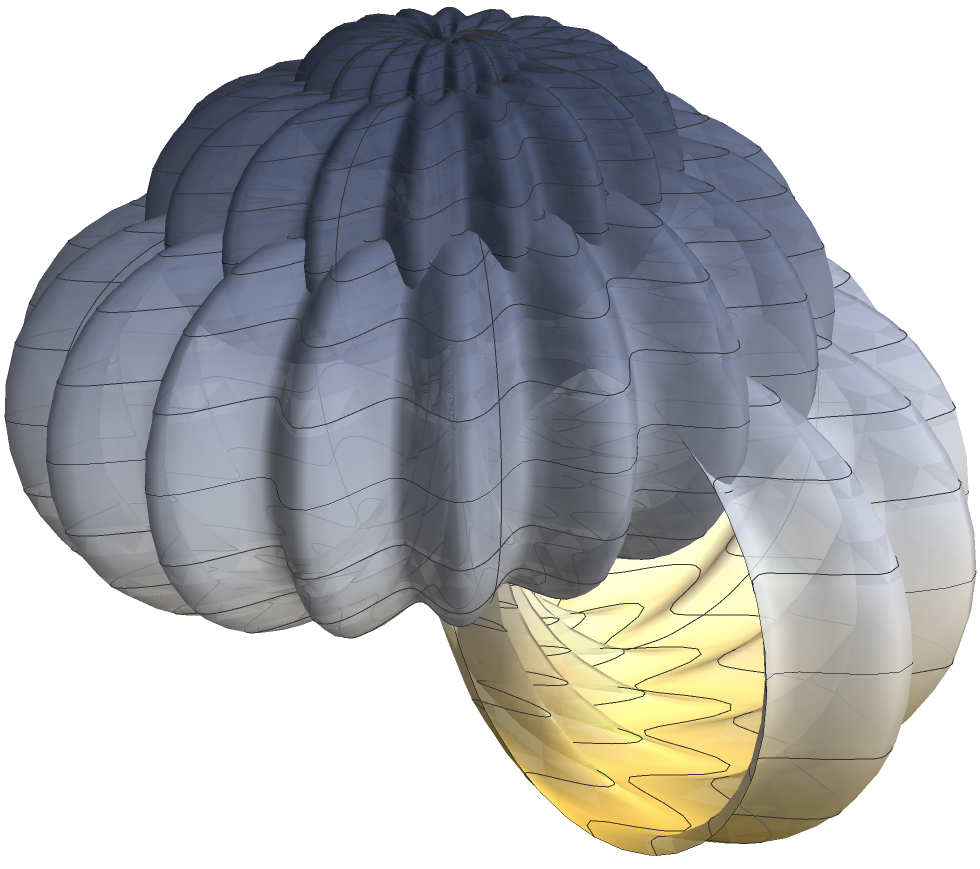
(* radius of tube *) xradius = 1; (* number of turns *) xturns = 4.6; (* height *) xheight = 2.5; (* wave frequency *) xWaveFreq = 80; (* wave amplitude *) xWaveAmplitude = 0.2; (* power *) xpower = 1.9; xf = Function[x, (x/(2*Pi)*xradius)]; shellF = Function[{u, v}, {xf[u]* Cos[xturns*u]*(1 + Cos[v] + Cos[xWaveFreq*u]*xWaveAmplitude), xf[u]*Sin[ xturns*u]*(1 + Cos[v] + Cos[xWaveFreq*u]*xWaveAmplitude), xf[u]*Sin[v] + xheight*(u/(2*Pi))^xpower}]; ParametricPlot3D[Evaluate@shellF[u, v], {u, 0, 5}, {v, 0, 2 Pi}, PlotPoints -> {160, 10}, PlotRange -> All, ColorFunction -> "GrayYellowTones", BoundaryStyle -> Directive[Black, Thin], PlotStyle -> Directive[White, Opacity[0.9], Specularity[10, 20]], Lighting -> "Neutral", Boxed -> False, Axes -> False]
Wentletrap
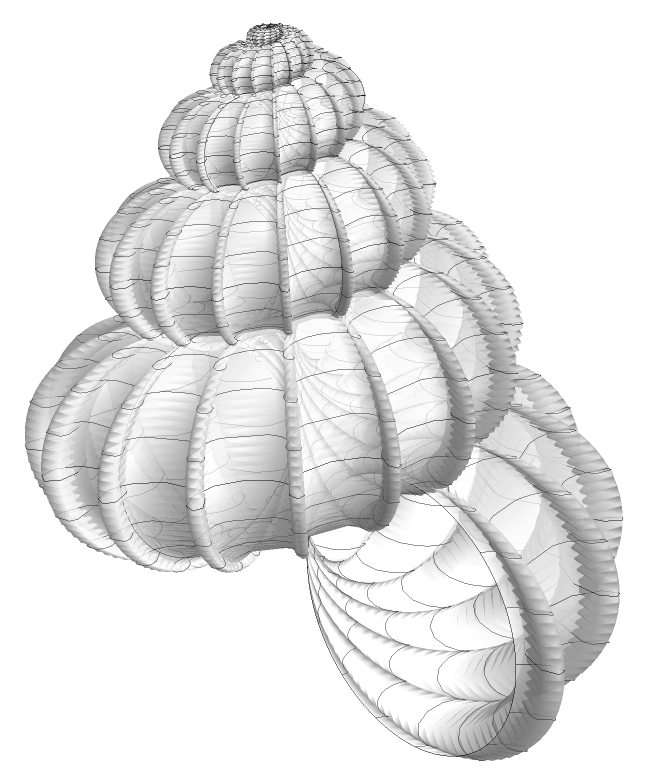
Clear[cW, seashell, cN, cH, cP, cA, cF] cN = 6.6; ("number of turns"); cH = 4.0; ("height"); cP = 2; (" power "); cA = 0.12;(" Ridge Amplitude "); cF = 15;(" Ridge Frequency "); cW = Function[(#/(2 Pi))^#2 ]; seashell[u_, v_] := {cW[u , cP] (Cos[cN u] - cA Cos[cN cF u]) (1 + Cos[v]), cW[u , cP] (Sin[cN u] + cA Sin[cN cF u]) (1 + Cos[v]), cW[u , cP] Sin[v] + cH (u/(2 Pi))^(1 + cP)}; ParametricPlot3D[ Evaluate@ seashell[u, v] , {u, 0, 6}, {v, 0, 2 Pi}, PlotPoints -> {200,40}, Axes -> True, Boxed -> True, BoundaryStyle -> Directive[Black, Thin], PlotStyle -> Directive[White, Opacity[0.7], Specularity[10, 20]], PlotRange -> All, Lighting -> "Neutral" ]
Gallery of Shapes
Tightness of Spiral
Outline Variations
Ribs and Folds
Spikes
Internal Structure
Analysis of Seashell Shapes
Seashells are showcasing of spirals. There are great variety of spiral shapes. Suppose we start with a circle winding around a spiral.
• The circle's shape changes periodically like a sine function, creating a corrugated shell somewhat emulate that of
• If instead of a circle we have a triangle, we can simulate that of
• If the rounding shape periodically changes shape to have spikes, then we might emulate shells that have horns such as the
or
• The periodic change might also emulate those shell having ribs such as the
References and Sources
The Algorithmic Beauty of Sea Shells , by Hans Meinhardt, Przemyslaw Prusinkiewicz, Deborah R Fowler. Buy at amazon
Mike Willams has sent me various formulas, see Math Parametric Equation for Seashell
 Seashell: Tusk Shell
Seashell: Tusk Shell Seashell: Common Screw Shell
Seashell: Common Screw Shell Seashell: Top Shell
Seashell: Top Shell Seashell: Spindle Shell
Seashell: Spindle Shell Seashell: Misc Seashells, Cut-in-Half View
Seashell: Misc Seashells, Cut-in-Half View Seashell: Conus Striatus Shell
Seashell: Conus Striatus Shell Seashell: Tooth Shell
Seashell: Tooth Shell Seashell: Misc Seashells, Cut-in-Half View
Seashell: Misc Seashells, Cut-in-Half View Seashell: Harper Shell
Seashell: Harper Shell Seashell: Black Murex Shell
Seashell: Black Murex Shell Seashell: Paper Nautilus Shell
Seashell: Paper Nautilus Shell Seashell: Pink-mouthed Murex
Seashell: Pink-mouthed Murex Seashell: Spider Scorpian Shell
Seashell: Spider Scorpian Shell Seashell: Venus Comb shell
Seashell: Venus Comb shell Seashell: Misc Seashells, Cut-in-Half View
Seashell: Misc Seashells, Cut-in-Half View Seashell: Misc Seashells, Cut-in-Half View
Seashell: Misc Seashells, Cut-in-Half View Seashell: Misc Seashells, Cut-in-Half View
Seashell: Misc Seashells, Cut-in-Half View Seashell: Misc Seashells, Cut-in-Half View
Seashell: Misc Seashells, Cut-in-Half View Seashell X-ray Photos
Seashell X-ray Photos Seashell X-ray Photos
Seashell X-ray Photos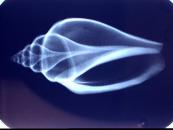 Seashell X-ray Photos
Seashell X-ray Photos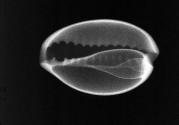 Seashell X-ray Photos
Seashell X-ray Photos