Spiric Section (work in progress)
History
Studied by Greek mathematician Perseus around 150 BC.
Description
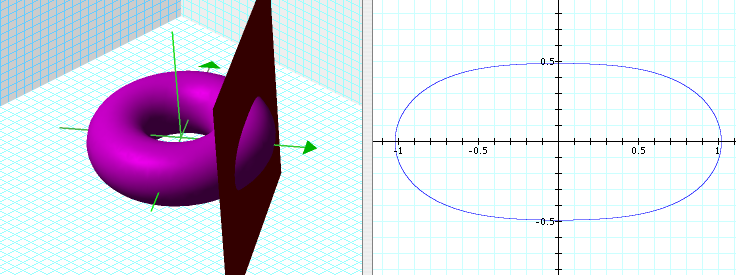
Spiric Section is the name given to a family of curves formed by the intersection of a torus and a plane that is parallel to the axis of the torus. That is any cross-sections of a donut sliced by a knife straight from top.
Formula
Cartesian equation: -a^2 + b^2 + c^2 + x^2 - 2*b*Sqrt[c^2 + x^2] + y^2 == 0 where a is the radius of the generating circle. b is the axis to the center of the generating circle. c is the distance from the plane to axis.
We want to elimate redundant parameters so that remaining parameter still generate all possible shapes of the curve. Since the shape of a torus is defined by the ratio of a and b, we can set b to 1, and let a be from 0 to b. Thus, the new equation for spiric section is: 1 - a^2 + c^2 + x^2 - 2*Sqrt[c^2 + x^2] + y^2 == 0 with parameter limited to 0 to 1.
Now, how we want eliminate this parameter boundary. How do we find a mapping from interval [0,Infinity] to [0,1]? (preferabbly linear and algebraic, but that's not possible.)
Cassinian ovals are special cases of Spiric sections.