Cassinian Oval
History
Studied by Giovanni Domenico (1680) in relation to motions of earth and sun.
Description
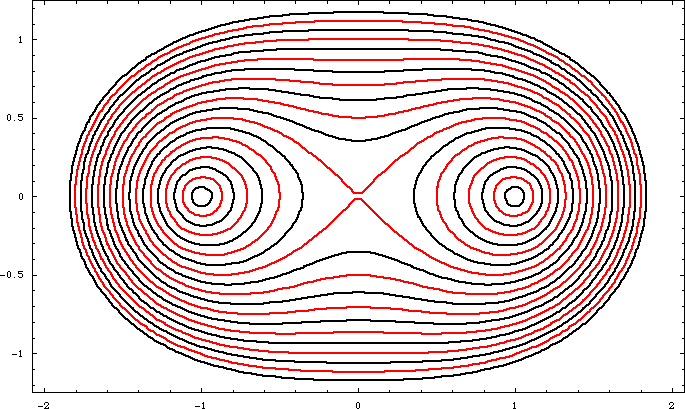
Cassinian oval describe a family of curves. Cassinian Oval is defined as follows: Given fixed points F1 and F2. Given a constant c. The locus of points such that distance[P,F1] * distance[P,F2] == c is cassinian oval.
Cassinian oval is analogous to the definition of ellipse, where sum of two distances is replace by product.
The fixed points F1 and F2 are called foci. Let the foci be {a,0} and {-a,0}. Let the constant c be b^2. The distance from a point {x,y} to another {m,n} is Sqrt[(x-m)^2+(y-n)^2]. Thus the equation for cassinian oval is Sqrt[(x-a)^2+y^2]*Sqrt[(x+a)^2+y^2]==b^2
When the square root of the constant c is less than half the distance between the foci, then there are two branches of the curve. In other words, if b < a, then there are two ovals. When a==b, the curve is called lemniscate of Bernoulli .
Formula
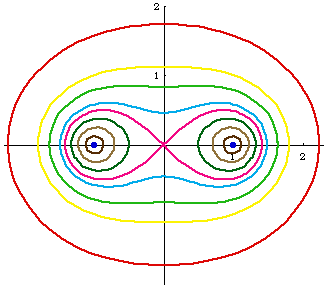
- Parametric: Sqrt[M/2] * {Cos[t], Sin[t]} where M is 2 *a^2* Cos[2 t] + 2 *Sqrt[(-a^4+b^4) + a^4 Cos[2* t]^2], 0 < t ≤ 2 π, and a < b. (This parametrization does not generate the complete curve when a > b.) derive parametric form of Cassini oval.
- Polar: r^4 + a^4 - 2 * r^2 * a^2 * Cos[2 * θ] == b^4.
- Bipolar: r1 * r2 == b^2.
- Cartesian: Sqrt[(x-a)^2+y^2]*Sqrt[(x+a)^2+y^2]==b^2.
Properties
Cassinian Oval as a Surface
Torus cut
Cassinian ovals are the intersection of a torus and a plane in certain positions.
Let c be the radius of the torus tube. Let d be the distance from the center of the tube to axis of the torus. The intersection of a plane c distant from the torus's axis is a Cassinian oval, with a = d and b^2 = Sqrt[4]*c*d, where a is half of the distance between foci, and b^2 is the product constant.
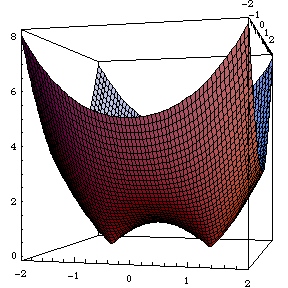
One thing we realize is that for Cassinian oval with large constant b^2, the curve approches a circle, and the corresponding torus is one such that the tube radius is larger than the center to directrix. That is, a self-intersecting torus without the hole. This surface also approaches a sphere.
Note that the toris in the figure below are not identical. Arbitrary vertical slice of a torus are not Cassinian ovals, they are called Spiric Sections .
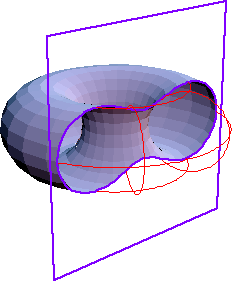
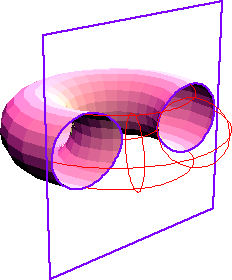
Proof outline: start with a torus equation (Sqrt[x^2 + y^2] - d)^2 + z^2 == c^2. Eliminate the square root and regroup to one side. Replace d=a and c = b^2/(Sqrt[4]*a). Now do the same with cassian oval implicit equation Sqrt[(x-a)^2+y^2]*Sqrt[(x+a)^2+y^2]==b^2. Luckly, one sees that the two equations match without further algebra considering scale and rotation of the curve. (detailed proof)
Related Web Sites
See: Websites on Plane Curves, Plane Curves Books .
Robert Yates: Curves and Their Properties .
The MacTutor History of Mathematics archive
Visual Complex Analysis by Tristan Needham. p 60 - 63. Buy at amazon He also mention curves formed by the locus of points whose product of distances to n points are constant.