The Problems of Traditional Math Notation
From Wikipedia Curvature as of :
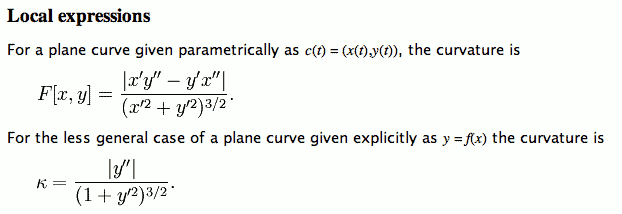
There are several problems in the notation used in above paragraph.
- The equation sign is used ambiguously. (for definition and for equality)
- The bracketing placement of symbols for absolute value, is not a matching pair, thus is ambiguous (when nested or sequential).
- The parenthesis and square bracket are used ambiguously. (used for order of operator application, also used as the parameter delimiter of a function.)
- The derivative notation of writing “ x' ” to mean the derivative of the function “x(t)” is ambiguous.
Traditional math notation has a lot problems. Inconsistencies and ambiguities. It lacks a grammar.
• the absolute sign is ambiguous because it is not a bracket. For example, ||c||a|b| is ambiguous. This also includes the Norm or Length notation of double vertical bars, for example, ‖z‖.
• the various parentheses ( ) [ ] { } are used
promiscuously. Sometimes for function parameters, sometimes for
operation priority in infix notation, and the different types are used
interchangeably. So, for example, f(x+y) can be interpreted as a
function “f” with argument “x+y”, or “f” times “x+y”.
• the notation for differentials “dy/dx” rapes the division notation. The differential notion has no position in math regarded as a computer language, as implied by the math philosophies of formalism and logicism.
• the equality sign “=” is used for several different purposes: assignment, definition, identity, equality indicator of a equation. Depending on the math context (say logic), it causes miscommunication and errors. (For example, in computer languages programing, often it's beginner's error to confuse “=” and “==”.)
• the placement of superscript for power is not consistent. e.g.
x2 but
sin2(x) for
(sin(x))2
The bottom line is, that math notation system as used by mathematicians although is invaluable and it is not sensible to say that we need to abolish it for something completely new just because there are some logical flaws, but as we go into our computing age where machines can process symbolic math and even does mathematics to some degree as of today (as in programing languages, Computer Algebra Systems and Theorem Proving systems), the shortcoming of traditional notation becomes apparent and unsuitable and needs to be mended.
Traditional does not mean Best
Traditional Math notation is the result of years of refinement. It is “survival of the fittest”.
Naturally evolved system does not mean optimal. Music notations with its 5-bar starves is another example. People will resist change because of inertia, either by habit or by existing literature. Math notations itself has gone thru changes big and small. I'm sure today's mathematicians will abhor at the notations used few centuries ago. (and then there were Roman numerals, whereas the decimal notation met with strong resistance) I believe that the “StandardForm” introduced in Mathematica is a change for the better. It is not adopted simply because it is proprietary and its creator Stephen Wolfram made himself disliked.
I believe Knuth himself has suggested change to the Summation notation, by putting the whole “i,imin,imax” to the bottom of the summation sign. That itself hasn't been adopted for reasons, not because it is unsound.
Inconsistencies of Traditional Math Notations
Some mathematicians do not like Mathematica's notation. This is partly because Mathematica is a functional programing language, and most people are unfamiliar with it. (the languages most people grew up with like C, Pascal, Java are called “imperative languages” by computer scientists.) I happen to be a strong disciple of functional programing. And, I'm a strong defender of the logic behind the Mathematica notation system, apart from my love functional programing paradigms.
Even before i appreciated Mathematica's notation, i have found traditional math notations to be quite inconsistent. In combination with my development into extreme logical thinking, i have problems using some of the traditional notations, because taken as is they generate contradictions if we regard formulas in them as a notations in a logical system. For example, the parenthesis is used as a grouping construct as in (3+4)*2 but also for enclosing function's arguments such as f(x)=sin(x). The equality sign “=”, had multiple meanings depending on the context. It sometimes is used to define, while other times to signify equivalence relation. When equal sign is used for identities, a example of logical problem that comes to my mind is the “level of equality”. For example, symbol substitution is obviously not the same as stating a theorem, and a definition may not be the same thing as a notational convention.
As one can see, there are lots of things are assumed in written math. As math history shows, many paradoxes or problems often traces back to subconscious implicit assumptions, only after identification and analysis are the issues resolved satisfactorily. (for example, irrational numbers, non-Euclidean geometry, complex numbers, understanding of real numbers (transcendental, algebraic), negative numbers, random numbers.). That is to say, many important thing in math became understood only after a serious understanding of the foundational issues. For example, calculus is fret with doubts until the concept of limits rests on logical understandings. Complex numbers are not developed until the puzzling “imaginary number” mysteries fully understood as a mere a 2-number pair numbering system. Negative numbers, irrational numbers, and the transfinite number concept all went thru similar routes that caused crisis or resistance and stagnation.
Another illogical convention is writing “sin2(x)” instead of the more logically consistent sin(x)2. The one i hate the most is the dy/dx notation. This notation is the epitome of traditional maths i hate so much. The dy/dx notation is the opposite of formalism. It entails the so-called concept of “differentials” and with a false division symbol. When using dy/dx notation in formulas, one really has to treat formula manipulation as manipulation of concepts at every step. Thinking programmatically creates problems. To me, when i see dy/dx, i think of it as a function of one variable that is the (mathematically defined) derivative of the function with one variable y. However, this mathematically significant interpretation usually doesn't make sense with whatever the text is trying to communicate. And when texts takes the dy and dx apart or discuss differentials, i really have a hard time understanding what is the mathematical content the author tries to convey. (if any).
The “d” in dx is a “meaningless” kludge. It functions as a delimiter more than anything else.
It is true that there are so much math that one cannot aim for one consistent notation to be used for all fields of math. However, certain elements can be improved, and I believe the Mathematica Standard form embodies many examples. Among the thing that is useless, is the italicizing of variables.
Math notation, like natural languages, is in a way very inefficient. One are bought up with it painfully and eventually become comfortable and swear by it. When encountering simpler and logical constructions that are novel, finding it “unnatural” and resistance is the common reaction.
That is, given two function f[t] and g[t], and for any given t we have a pairs of numbers {f[t],g[t]}…
Here, f[t] is used in one place to represent a function, but in another place used to represent its value.
In the Wikipedia article Golden ratio, quote:
Two quantities a and b are said to be in the golden ratio φ if:
(a+b)/a = a/b = φThis equation unambiguously defines φ.
This is a example of abuse of math notation.
In (a+b)/a = a/b = φ, we have basically a system of equations
of 3 variables. The reason someone wrote this equation to define the
golden ratio, is due mostly to the abuse of the equal sign as used in
traditional math notation. In fact, the equation does not make sense.
This abuse does not happen just in Wikipedia, but in just about every math textbook from professional mathematicians. (e.g. Visual Complex Analysis, by Tristan Needham. Buy at amazon or my friend's Differential Equations, Mechanics, and Computation Buy at amazon)
Typically, mathematicians will just say it doesn't matter, because by context it makes it clear to humans. I disagree. I think it introduces lots of mis-understanding and garbage into our minds, especially those who have not studied symbolic logic and proof systems (which, is actually majority of mathematicians). The wishy-washy, ill-defined, subconscious, notions and formulas make logical analysis of math subjects difficult. Of course, mathematicians simply grew up with this, got used to it, so don't perceive any problem. They'd rather attribute the problem to the inherent difficulty of math concepts. I think that if we actually force all math notations into something similar of a formal language (in Hilbert's formalism sense), then many un-necessary confusion will go away, and math understanding and research will be easier and grow faster. (one historical example to illustrate this is the history of complex numbers and calculus, which took decades to overcome.)
You will realize much of these problems when you actually try to program math to computers, may it be setting up a computer based proof or writing a simple computer algebra software. For example, let's say you want to write program to draw a rectangle of golden ratio. You read about the golden ratio. You need to define it in your program. You start with the Wikipedia equation given, then immediately, you'd realize, it does not make sense at all. Because when you try to program something to the computer, the computer won't accept your wishy-washy subconscious ill-defined implicit human notions. When you actually try to program it, you'll realize lots of these issues, and in fact come out with a clear understanding of the subject, even if the subject is a basic one such as a definition of a number.
If you do a lot math programing or working in proof systems, you realize that what's said in math textbook and what needs to be written as a program are very incongruous. For example, try translating the descriptions of how to do derivatives in calculus textbooks into a computer program. (note: this issue is not about the deep subject of mathematical definition by “what is” vs algorithmic definition by “how to”.)
Further Readings
- Functional Mathematics , by Raymond Boute. http://www.funmath.be/
- Wikipedia: Abuse of notation
- How Computing Science created a new mathematical style By Edsger W. Dykstra (EWD 1073) , by Edsger W Dijkstra. EWD1073.html
- Under the spell of Leibniz's dream , by Edsger W Dijkstra. EWD1298.html
- On the desirability of mechanizing calculational proofs , by Panagiotis Manolios, J Strother Moore.
- Functional declarative language design and predicate calculus: a practical approach , by Raymond Boute (INTEC, Ghent University, Belgium, Ghent, Belgium). http://portal.acm.org/citation.cfm?id=1086642.1086647
- Formalized Mathematics , by John Harrison. http://www.rbjones.com/rbjpub/logic/jrh0100.htm
- ODE notation considered harmful By ?. @
http://stochastix.wordpress.com/2012/06/05/ode-notation-considered-harmful/