Abuse of Math Notation

Differential dy/dx

the notation for differentiation is exemplary of the idiocy of math notations. Among which, the leibniz dy/dx is worst. Best is Euler's D[y]

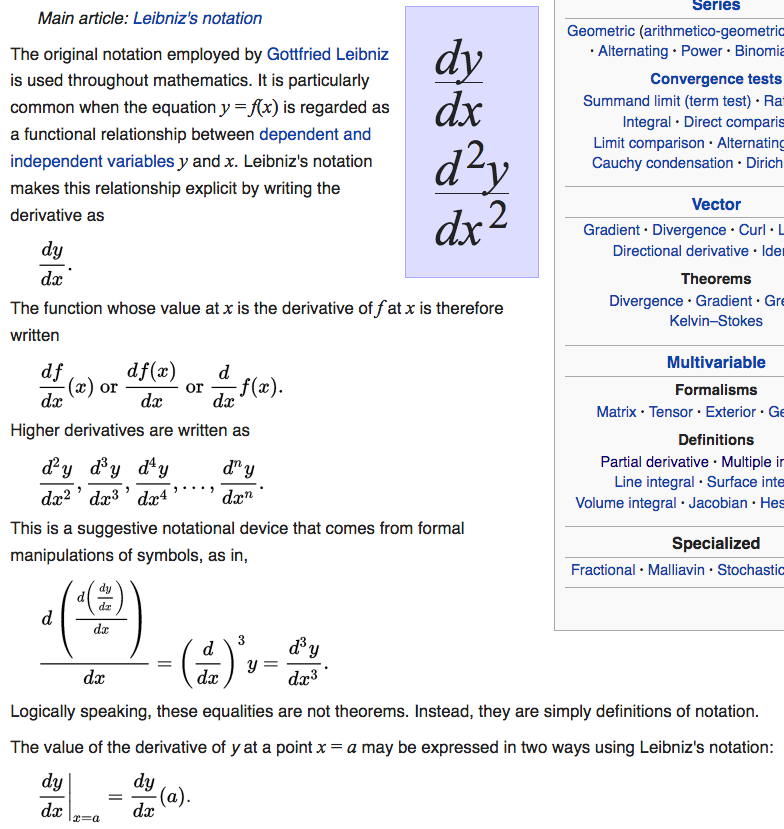
Wikipedia Notation for differentiation

Let's look at dy/dx. Here's inconsistencies:

• is dy meant to be d * y, 2 variables? or, is d supposed to be an operator? Note that normaly, when 2 letter are adjacent such as xy, it means x * y.

• in dy/dx, sometimes the y is meant to be a variable, sometimes it's a function. The interpretation, is, “flexible”.

• now, look at the dx in dy/dx. If that y is a function, why isn't the x a function?

• now, the diversion sign / is used. Ok, that part we can take standard analysis to explain as actual division.

• now, sometimes partial derivative is written as δy/δx. Now, it's strange, when one of the symbol is replaced by another symbol, the meaning of the entire thing changed!!

so, basically, what am saying, is abuse of notation. But even if no abuse of notation happens, the traditional math notation is pretty much pictograph that takes conditioning to understand, lacking a grammar, comparable to natural languages such as English. Full of quirks and idioms.

Most mathematicians, don't have these problems, don't see these problems. But computer scientists do, or any programer. As soon as one tries writes to code it into program, lots problem arise.

one simple example is distinction of equality, definition, assignment, and identity, and notational equivalence! In traditional math, they are all just =. In general purpose programing languages, at least we have = for assignment and == for equality testing.

Here, the equation sign got fk'd.

here, it's used for equality or equivalence of notation, not meaning.

this is besides the usual abuse of identity, definition, and real equality.

it's from Wikipedia, 2017-10-08, at Partial derivative

look at that φ.

Normally, the notation for function's domain codomain takes the form of

we have 5 symbols, from left to right are

1. symbol representing the function
2. Colon as separator
3. Symbol representing the domain (a set)
4. right arrow as a separator between domain and codomain
5. Symbol representing the codomain (a set)

But here, the domain is now M ⊃ Wᵢ

What is that? that's a relation between sets, not a set.

So, this relation, is the domain of f. WTF?

math notation is pictograph

am now think that the entire traditional math notation should be abolished. Absolutely. There's zero goodness in it.

traditional math notations, they work as pictographs. Or, as picture abbrev of words.

this includes dy/dx, x^2 sin^2, ∫ f dx, ∂ Δ ∇, matrix … ⋱, set builder {x | x ≻ 0, x ∈ ℤ}, f:ℝ²→ℝ³, all just pictographs

pictographs, such that each need to be memorized. Its somewhat composable, but meaning changes somewhat or drastically. no grammar.

why is traditional math notation still useful? because, pictograph is still often better than just words, e.g. emoji 😒 😤 🤢

but once you realize the nature of traditional math notation, i.e. pictographs, emoji, you want to throw it out. All of it.

actually, Math notation is not simple pictograph as emoji. It has larger shape. e.g. ∑ with bottom/top lines, matrix as array, big ∫ symbol, big fraction line, etc.

still, the nature of traditional math notation is basically somewhat structured n losely defined pictographs serving primarily as abbrev of words.

this is PART of the reason, that math notation as expression in computer languages is totally incompatible/hard.

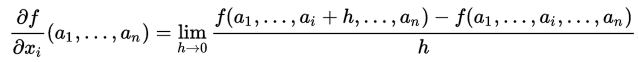
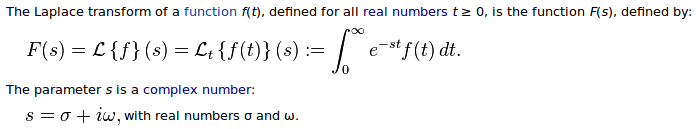
first of all, note the ambiguous use of the brackets. The curly bracket is used as the delimiter for formal parameter of a function and also as delimiter for formal parameter of a expression. The round bracket is also used as delimiter for formal parameter of a function.

then, notice that this definition tries to do several things:

• definition of Laplace transform
• show notational equivalence
• mixed nonsensical use of equal sign and define sign. (1) the equal sign is used for definition of notational equivalence. (2) The left side of the definition is a equation. It seems to define a equation by a integral. (3) lastly, the integral notation is all eff'd up with that “dt” thing. There's no variable named d here.
• illogical and extraneous use of variables. Here, there's a confusing change of variable from “t” to “s”, even though we are defining a function of one variable, there is no need to mention its formal parameter.

in general, mathematicians use math notations like a diagram of pictographs, the same way children draw pictures to express meaning. The output thereof, is not grammatically coherent. We understand them by years of convention and context and guess-work.

better:

ℒ[f[x]][s] := ∫[ ⅇ^(-s*t) * f[x],{x,0,∞}]