Syntactic Meaning of Variable (2018)
when you have a expression like this
x == x
shoud it eval to true or false?
the bottom of the issue is, does a named variable/unknown represent a SPECIFIC value? If so, ‹x›==‹x› is true. but if ‹x› represents any unknown (such as arbitrary string in a formal language), not specific, then ‹x›==‹x› can be true or false.
In traditional math notation, a variable ‹x› (consider ‹x› as italized x), usually means a specific value. So, mathematicians would write reflecive property as x = x. So, here, variable/symbols of the same name means the same value. (thus, in our context, ‹x›==‹x› is always true.)
in BNF system, variable is called non-terminal, and traditionally written as all caps, e.g. X. So, whether X is equals to itself, depends on what eventual terminals are used to replace X. So, X == X can mean true or false. (in our context, that means, ‹x›==‹x› can be true or false.)
In Wolfram Language, pattern matching system, a named pattern has a specific value. So that means, ‹x›==‹x› is always true.
my interest is originally from writing docs. eg i want to say
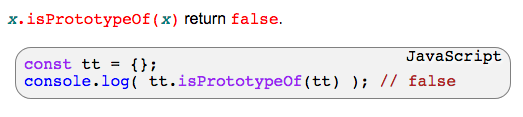
see JS: Object.prototype.isPrototypeOf
but that depends on what the notation ‹x› is meant.
In racket lisp language's documentation, it also uses italized text for variable, extensively, and thus have the same issue.
example:
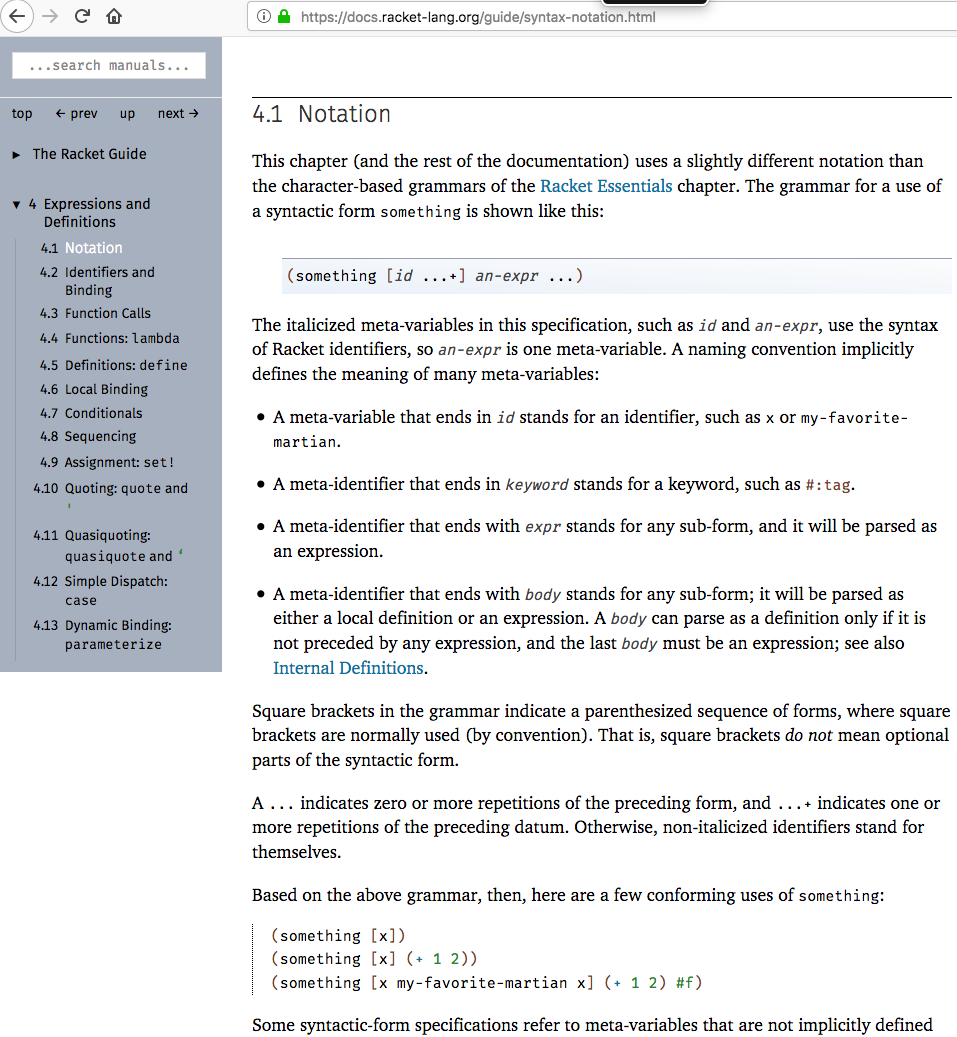
but i haven't seen occassions of ‹x›==‹x› occur to determine what is the italized notation means exactly.
so, i wanted to think about, look at, explore, what system of formal lang or meaning of a italic var should be defined, pro and cons, etc. eg look at coq idris etc. it's not a problem i actually need to solve, but alone the way with my study of proof systems/formal lang.
so am wondering, what's the similar situation/system if any, used in coq, idris, agda, etc to represent a variable, unknown, or meta variable (as the Racket lang doc discussed.).
Systematic Grammar
- Why Syntax is More Important Than Semantics (2020)
- Formal Definition of Systematic Grammar (2016)
- Grammar Complexity of conlang and complang (2016)
- Composable Syntax (2016)
- Syntax Algebra (2016)
- Syntactic Meaning of Variable (2018)
- OCaml Syntax Sucks (2016)
- Problem of Expressive Programing Languages (2021)
Sigils war, special chars in variable names as syntactic type system
- Variable Naming. English Words Considered Harmful
- The Sigil War, Syntactic Indicator for Types of Function and Variable (2016)
- Function Parameter names start with phi φ, variable names start with xi ξ (2014)
- Emacs Lisp Coding Style. DOLLAR SIGN $ and AT SIGN @ in Variable Names
- Jargon: Predicate in Programing Languages (2014)
- Syntactic Meaning of Variable (2018)
- Perl: Variable Name Prefix (aka Sigil)
- Ruby: Variable Name Conventions
- PowerShell: Variable
- Clojure: Variable Name Conventions (sigil. macro magic characters.)