Geometric Inversion, 2D Grid

geometric inversion of a 2d grid

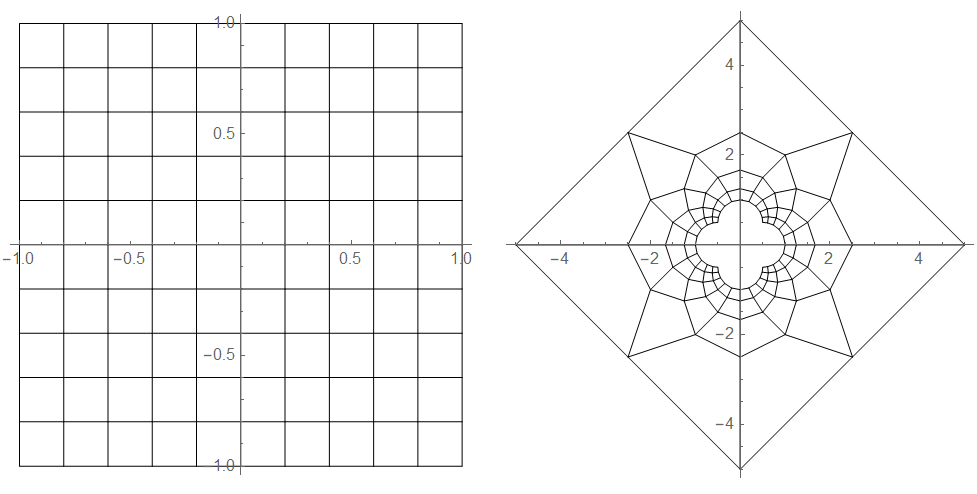
geoInv = ((With[{x662 = #.#}, If[ x662 < 0.00000001, #, #/x662] ]) &);
cArray = CoordinateBoundsArray[{{-1, 1}, {-1, 1}}, Into[10] ];
hLines= (BlockMap[Line,#,2,1]&) /@ cArray;
vLines= (BlockMap[Line,#,2,1]&) /@ Transpose @ cArray;
gp1 = {hLines , vLines};
gp2 = gp1 /. Line[x_] :> Line[ geoInv /@ x ];
GraphicsGrid[{{Graphics[gp1, Axes->True ], Graphics[gp2, Axes->True ]}} ]

note that we apply the geometric inversion function on the grid points only, not on the lines themselfs. This results more artistic images. Normally, inversion of lines becomes circles, so you don't have the spider web kinda image.

[see Geometric Inversion]

geometric inversion of squares on grid

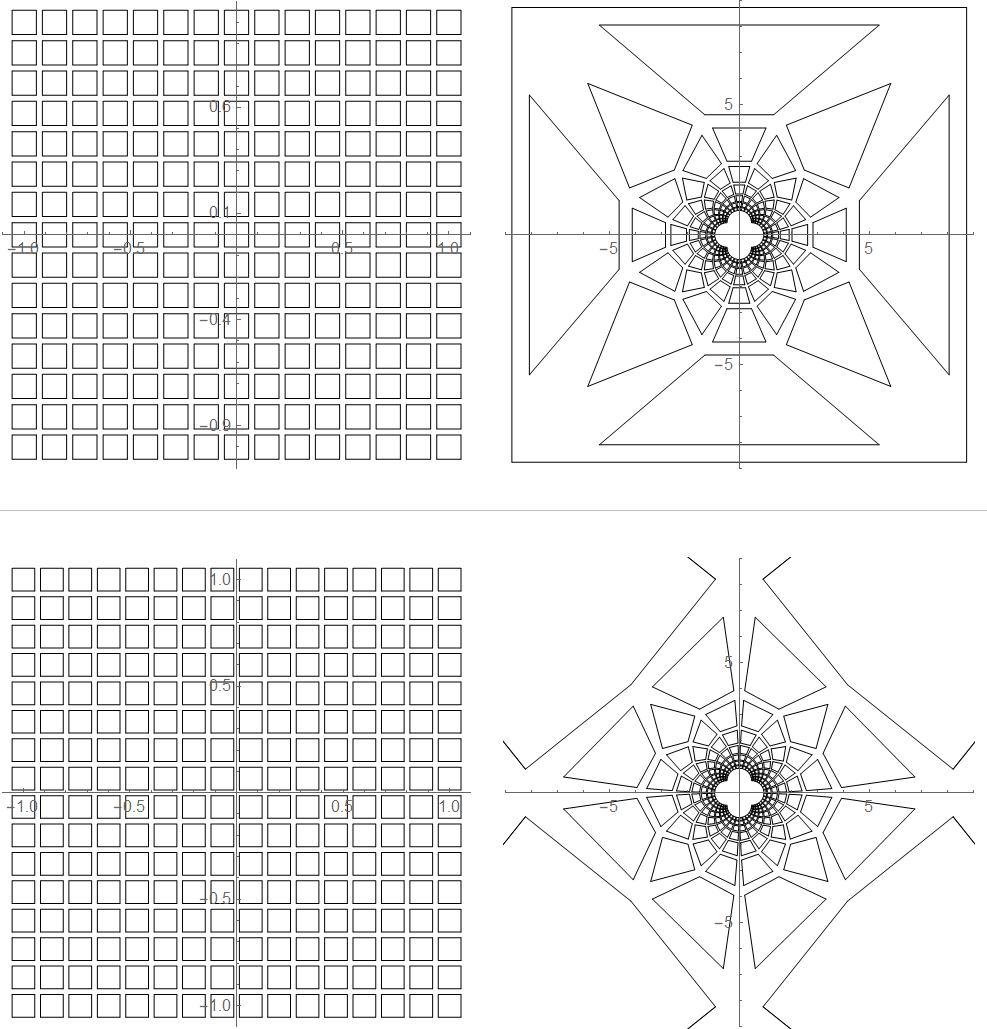
geoInv = ((With[{x662 = #.#}, If[ x662 < 0.00000001, #, #/x662] ]) &);

xRange=1;
gridDivN = 15;
δ=xRange 2/gridDivN;
sqWidth=δ * 8/10;
s=sqWidth/2;

squaresGP=
Table[
With[{ a={x-s,y-s},b={x+s,y-s},c={x+s,y+s},d={x-s,y+s}},
GraphicsComplex[{a,b,c,d},Line@{1,2,3,4,1}]
]
,{x,-xRange,xRange,δ},{y,-xRange,xRange,δ}];

gp2= squaresGP /. GraphicsComplex[x_, r__] :> GraphicsComplex[geoInv /@ x, r];

GraphicsGrid[{{Graphics[squaresGP, Axes->True ], Graphics[gp2, Axes->True, PlotRange->9 ]}} ]

geometric inversion of 2d grid, as tubes

geoInv = ((With[{x662 = # . #}, If[x662 < 0.00000001, #, #/x662]]) &)

lotsTubes =
  Table[Tube[{{x, y, 0}, {x + 1, y, 0}, {x + 1, y + 1, 0}, {x, y + 1,
      0}, {x, y, 0}}], {x, -5.5, 4.5, 1}, {y, -5.5, 4.5, 1}];
tubeGraphics = Graphics3D[lotsTubes]
geoInv = ((With[{x662 = # . #}, If[x662 < 0.00000001, #, #/x662]]) &);

ReplaceAll[tubeGraphics, Tube[pts_] :> Tube[geoInv /@ pts]]