Math: Counting Intersections in Honeycomb

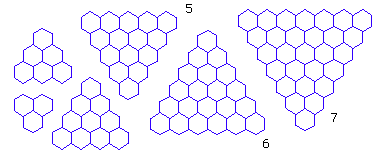
For example, we have:

• f(2) = 4
• f(3) = 10
• f(4) = 18

answer below
↓
↓
↓
↓
↓

↓
↓
↓
↓
↓

↓
↓
↓
↓
↓

↓
↓
↓
↓
↓

↓
↓
↓
↓
↓

↓
↓
↓
↓
↓

↓
↓
↓
↓
↓

↓
↓
↓
↓
↓

↓
↓
↓
↓
↓

↓
↓
↓
↓
↓

Triangular shaped board with n honeycomb on one side has 1+ 4*n + n^2 number of points where straight line meets (that is, counting the “bents” on the perimeter.) For example, if n=2, then we have 13 points.

If the perimeter bents are not counted, then the formula is -2+n+n^2. For example, if n=2, then we have 4 points.

let n be the number of hexagons on the side of a honeycomb grid with a triangle overall-shape.

By inspection, we have this recursive formula:

f[1] = 6
f[n] = f[n-1] + n*2+3

compute a few terms we see that:

f[2] = 6 + 2*2+3
f[3] = 6 + 2*2+3 + 3*2+3
f[4] = 6 + 2*2+3 + 3*2+3 + 4*2+3
f[5] = 6 + 2*2+3 + 3*2+3 + 4*2+3 + 5*2+3
…

from the above, we see a pattern, and it is:

f[n] = 6 + Sum[i,{i,2,n}] *2 + (n-1)*3

the value Sum[i,{i,2,n}] is 1/2 *(n-1)(2+n). So,

f[n] = 1+ 4*n + n^2

n and f[n] values list:

{1, 6}, {2, 13}, {3, 22}, {4, 33}, {5, 46},{6, 61}, {7, 78}, {8, 97}, {9, 118}, {10, 141}

Not Counting Edge-Bends

Now if the edge bent points doesn't count, By inspection we reduce each side by n*3 and 3 corners, so

f[1] = 0
f[n] = -2 + n + n^2

n and f[n] values list:

{1, 0}, {2, 4}, {3, 10}, {4, 18}, {5, 28}, {6, 40},{7, 54}, {8, 70}, {9, 88}, {10, 108}

Over-All Hexgonal Shaped Board

• A honeycomb grid with n hexagons on a side has 6*n^2 number of “intersections”, counting the edge bent as an intersection.
• A honeycomb grid with n hexagons on a side has -6*n + 6*n^2 number of “intersections”, not counting the edge bent as an intersection.

let n be the number of hexagons on the side.

By inspection, we have this recursive formula:

 f[1] = 6
 f[n] = f[n-1] + (2*n-1)*6

so:

 f[2] = 6 + (2*2-1)*6
 f[3] = 6 + (2*2-1)*6 + (2*3-1)*6
 f[4] = 6 + (2*2-1)*6 + (2*3-1)*6 + (2*4-1)*6
 f[n] = 6 + 6 * Sum[2*i-1,{i,2,n}]
      = 6 + 6 * (n^2-1)
      = 6 n^2

n and f[n] values list:

{1, 6}, {2, 24}, {3, 54}, {4, 96}, {5, 150}, {6, 216}, {7, 294}, {8, 384}, {9, 486}

if edges bent points doesn't count, then we simply minus 6*n. So,

 f[1] = 0
 f[n] = -6 n + 6 n^2

n and f[n] values list:

{1, 0}, {2, 12}, {3, 36}, {4, 72}, {5, 120}, {6, 180}, {7, 252}, {8, 336}, {9, 432}

Mathematica code: for hex grid 1: hex_board.nb; for hex grid 2: hex_board2.nb; triangular grid: tri_board.nb.

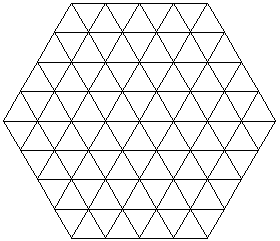
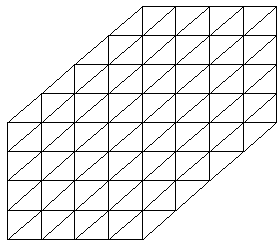
This board with edge size n has -3 n + 3 n^2 + 1 points.

With triangular outline board of size n.

By inspection, we have this recursive formula:

 f[1] = 1
 f[n] = f[n-1] + n

so:

 f[2] = 1 + 2
 f[3] = 1 + 2 + 3
 f[4] = 1 + 2 + 3 + 4
 f[n] = Sum[i,{i,1,n}]
      = 1/2 * n (1+n)
      = (n+n^2)/2

n and f[n] values list:

{{1, 1}, {2, 3}, {3, 6}, {4, 10}, {5, 15}, {6, 21}, {7, 28}, {8, 36}, {9, 45}, {10, 55}, {11, 66}, {12, 78}}

For hexagonal outline, simply multiply by 6 and substract 6*n for the repeated edges, than add the center back. So we have:

 f[n] = Sum[i,{i,1,n}] * 6 - 6*n + 1
      = -6 n + 3 n (1+n)
      = -3 n + 3 n^2 + 1

n and f[n] values list:

{{1, 1}, {2, 7}, {3, 19}, {4, 37}, {5, 61}, {6, 91}, {7, 127}, {8, 169}, {9, 217}, {10, 271}, {11, 331}, {12, 397}}

back to Go Board Game on Hexagonal and Triangular Grids