Go Board Game on Hexagonal and Triangular Grids

By Xah Lee. Date: 2003-12-30. Last updated: 2011-04-04.

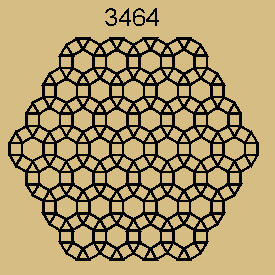
Honeycomb (hexagonal) grid

I have been thinking about the go board game played on various regular tilings. First experiment is the honeycomb grid (which has 3 connections per intersection), then i'm going to try triangular grid (6 connections), then i'll try some regular or semi-regular tiling with, many of which has 4 connections just like the rectangular grid but different topology.

In designing a honeycomb board, there are few issues to consider:

Whether the board center should be a intersection.
What should be the overall board shape? (hexagonal, triangular, or rhombus)
How the edges should be like? (and can it be played on?) (for example, in the regular board, the corner can be played on even though it's not a intersection)
How large should the board be?

honey comb grid — Illustration that shows different board design. The left two shows two different types of board edge layout. Also note that the overall shape can be hexagonal or triangular. And, some board have a vertex/intersection at the center.

I played with my brother two games, and it is quite interesting. The game is overly tactical, because every stone has only 3 connections (liberties). It's extremely easy to kill.

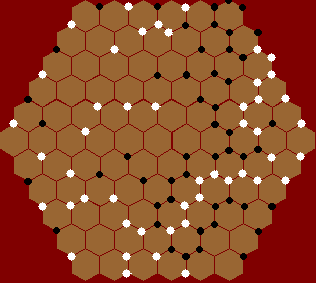
hex1 game — One game in progress. White to move.

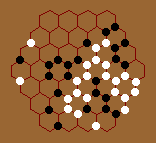
go game on honey comb board — game in progress. Black to move.

The edge points have strong advantage, because it takes 5 moves to capture in practice, while it takes 3 in center positions. If one tries to capture the edge point, he can be captured before he succeed. So, the edge points are somewhat invincible until endgame. It is most easy to make two eyes based on the edge. A good strategy seems to play on the edge first, then snake in. Perhaps the board should be modified so that the angular edge cannot be played. This can be done by either cutting the edge flat or allow only stones on intersections. This way, all points has 3 liberties.

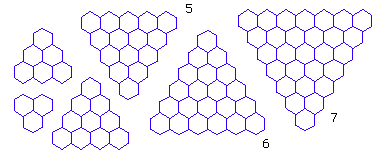
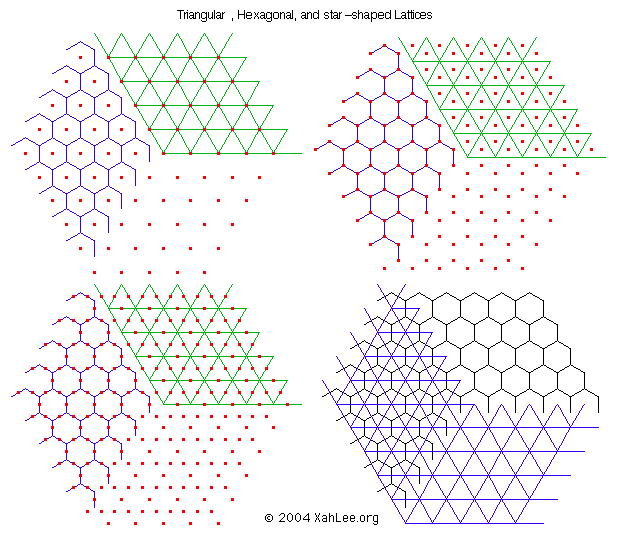
In drawing these boards, some math questions came up. Look at the triangular boards, which has sides from 2 hexagons to 7. Some of these has a intersection at the center, others a hexagon. What sizes will have a central intersection?

It turns out, for overal triangular boards, when the side of the board can be expressed as 2+n*3 or 3+n*3, then the board has a intersection at center.

Overall triangular shaped board with n hexagon sides has 1+ 4*n + n^2 number of intersections, counting the bent points on the sides.
Overall triangular shaped board with n hexagon sides has -2+n+n^2 number of intersections, NOT counting the bent points on the sides.

Overall hexagonal shaped boards with n hexagon sides has 6*n^2 number of intersections, counting the bent points on the sides.
Overall hexagonal shaped boards with n hexagon sides has -6*n + 6*n^2 number of intersections, NOT counting the bent points on the sides.

(Derivation: Math: Counting Intersections in Honeycomb)

Triangular Grid

Triangular grid has six liberties. My hexagonal grid study shows that best overall shape is probably as round as possible, so that edge-special play is minimized. So, we can just think about boards with a hexagonal border. The triangular grid can be deformed to a rectangular shape, equivalent to a rectangular grid with diagonals in one direction.

In contrast to the honeycomb grid, the triangular grid has 6 liberties, which makes it hard to capture.

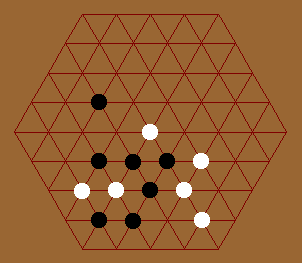
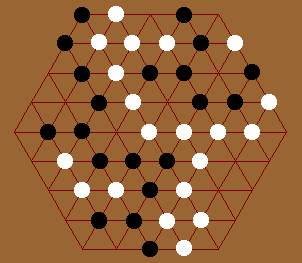
go on triangular grid — One game in progress. (black moves first) Left: white's turn. The two white stones on the left probably cannot be saved. Right: game ended. Black's turn.

In sharp contrast to the honeycomb grid, game on triangular grid is slow. In the honeycomb grid, life-and-death situation comes up frequently, and one has to think a lot. In triangular grid, this is not so. A good strategy in the honeycomb grid seems to be spreading pieces all over the board, while a good strategy on the triangular grid seems to be playing in just one connected group (snaking).

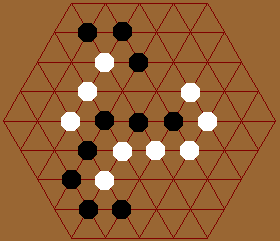
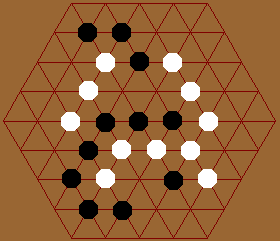
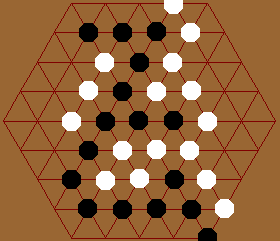
It seems that whoever builds a wall enclosing larger area wins. So, on a small board, playing center seems advantageous. The board should be increased in sized to increase its strategic appeal. The center spot might also be removed. One might also try to remove several spots on the board, like punching in holes. This however, is basically changing the topology of the board, which a systematic exploration can be taken. (That is, using regular tiling as grids.)

This board with edge size n triangles has -3 n + 3 n^2 + 1 points. (Derivation: Math: Counting Intersections in Honeycomb)

triangular, hexagonal, star, lattices — triangular lattice and the hexagonal lattice are duals of each other. Also note the star shaped lattice, formed by the mid-points of the triangular grid, or the mid-points of the hexagonal grid. The star-lattice makes a grid where each intersection has 4 degrees.

Other Grids

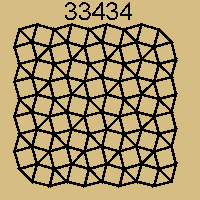
Here is a game on a grid called 33344 tiling that has 5 liberties per intersection. (game played using the freedgo program, highly recommended.)

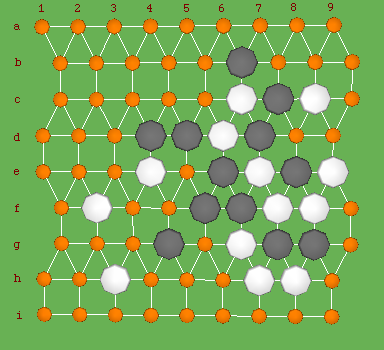
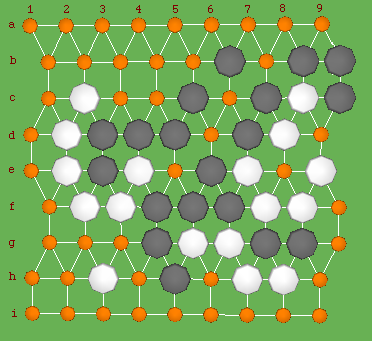
go game on a 33344 tiling — Black to play. c2.5 or d3 seems to be good moves.

Playing go on 33344 tiling feels more similar to traditional go, at least in local fight. Note the board above is a 9x9 board with a total of 81 points. This grid is equivalent to the square grid plus diagonal links on every other row.

3636 tiling — Various tiling. (image by Joao Pedro Neto. Used with permission. Source www.di.fc.ul.pt)

3464 tiling — Various tiling. (image by Joao Pedro Neto. Used with permission. Source www.di.fc.ul.pt)

go on a circular grid — “round go” by Harald Schwarz. ~~http://www.escape.de/users/shusaku/euro96/issue3/roundgo.htm~~

Thoughts On Go Board Variation

As we know, many games are played on various regular grids, such as checker, Chinese checker, gomoku (tic-tac-toe, connect four), go. The cellular automata Game of Life is also played on a rectangular grid. Many variations has been experimented, such as triangular grid and torus board. We can think about a systematical exploration of variations by changing the grid topology. The grid can be any of periodic or semi-periodic tiling, and we can change the global topology from a plane to sphere, torus, and all the possible 2 dimensional surfaces including non-orientable ones like Cross-Cap Surface (projective plane). The grid (connection) topology can be abstractly defined, to give us more variation and systematic exploration.

In writing a program that play these games, one may also make it modularized so that different boards, rules, topology, and AI can be written as a plug-in.

generalization of grids

In B Grunbaum and G C Shephard's Tilings and Patterns book Buy at amazon, it was proven that if we consider the topology of Archimedean tilings, there are 13 types only. (i may be off in terminology, see the book for detail) One should note that these are planar graphs. That is, when we consider only the topology aspects of a tilling, we are essentially regarding it as a graph, and a planar one. When we explore different boards of go or cellular automata, we are interested in the topological properties of the grid. So, for a abstract systematic exploration of possible (regular) grids, we have to consider not just (regular) planar graphs, but also non-planar ones. For example, consider the standard rectangular grid of the go game; if suppose each point are connected to its 4 diagonal neighbors as well. Now we have a (regular) graph where each vertex has 8 degrees. This grid cannot be drawn on a plane without crossings. So, here we are dealing with non-planar graphs that are “regular” in some sense. I think this is totally unexplored field.

Other Resources

[Other [Go] boards 2003 By Joao Pedro Neto. At http://www.di.fc.ul.pt/~jpn/gv/boards.htm , accessed on 2011-10-25 ]
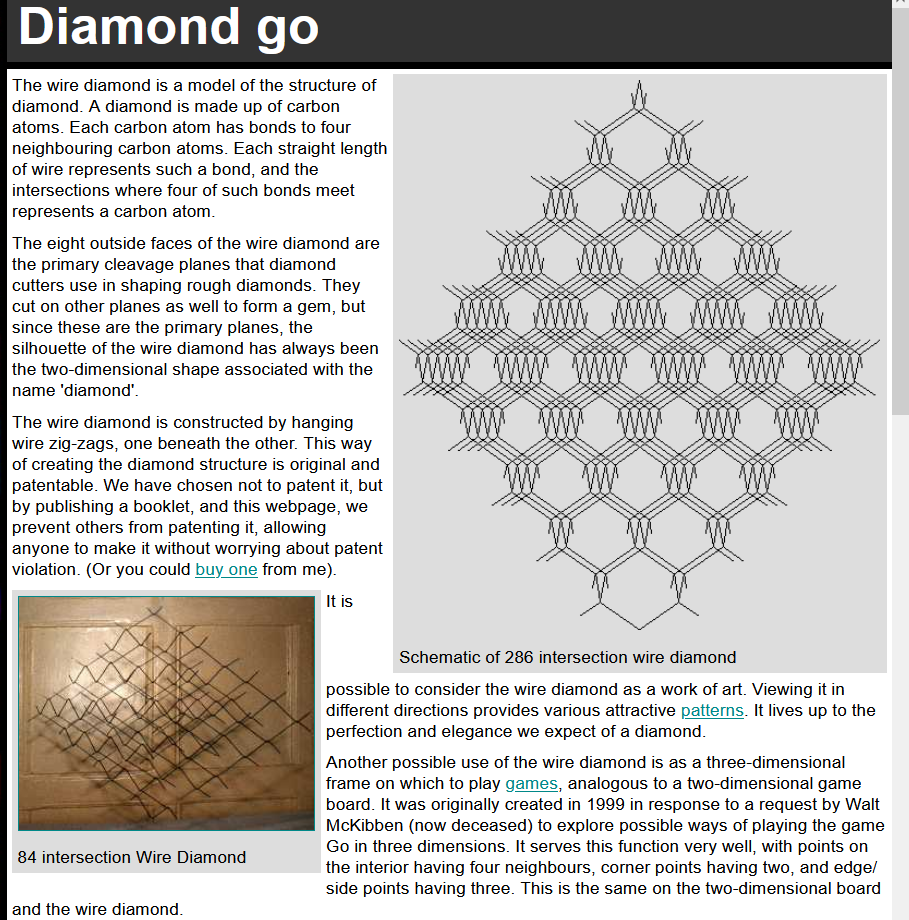
[Diamond Go 2006 By Henry Segerman. At http://www.segerman.org/diamond/ , accessed on 2011-10-25 ]
software to plays go on various 2D and 3D grids. [Free Go 2004 by Lewey Geselowitz. At http://www.leweyg.com/lc/freedgo.html ]

A article on go on hex and triangular grid, [A Family for Go. Abstract games issue 13 Spring 2003 2003-04-23 By Joao Pedro Neto, Bill Taylor. At ~~http://www.abstractgamesmagazine.com/go_variants.html~~]