Reading Notes on Nicolas Bourbaki
lots interesting details in the wikipedia bourbaki article. some of the greatest french mathematicians there.
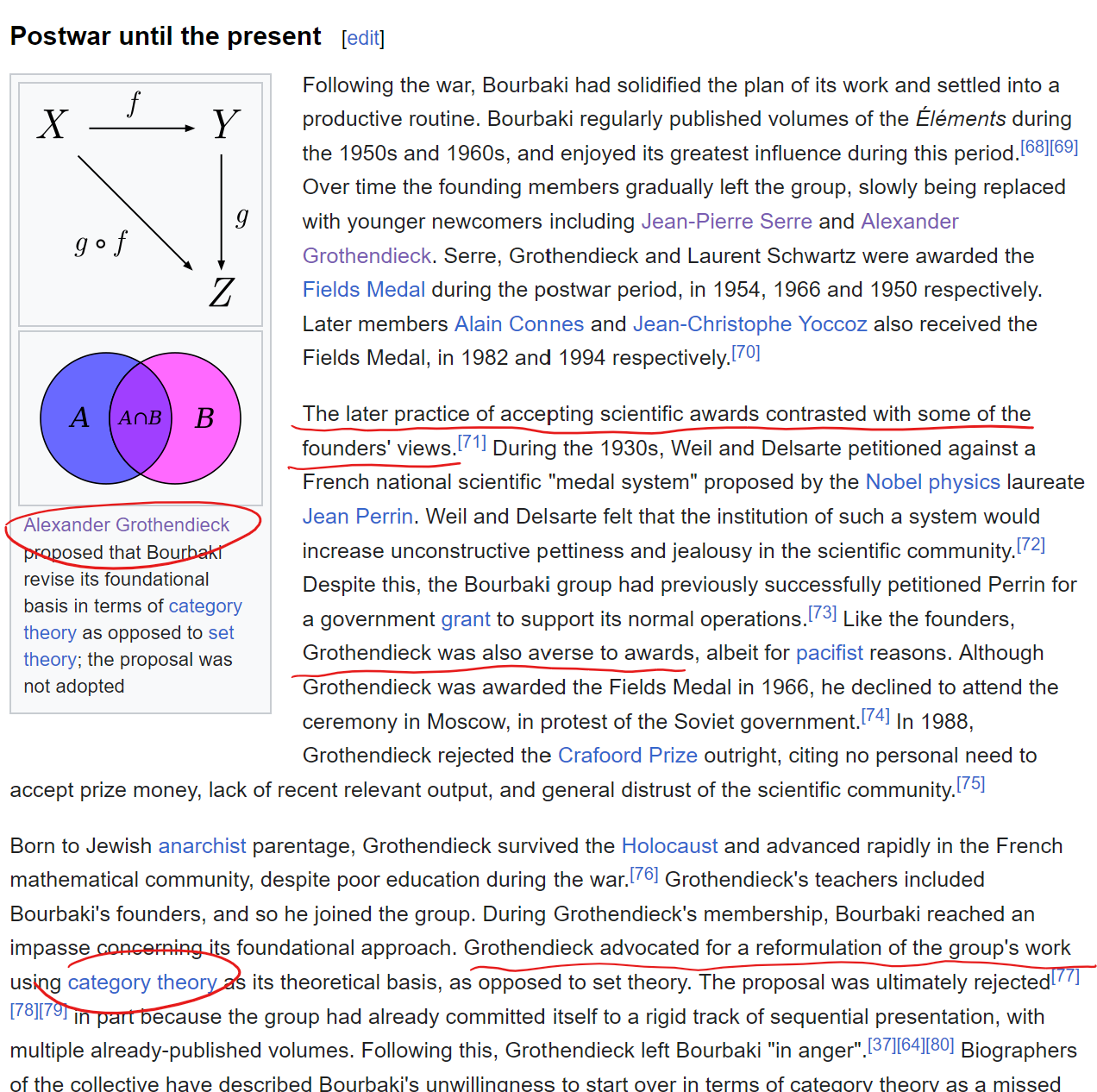
grothendieck, one of the greatest in human history, apparently left because they wouldn't do category theory.
Send your young mathematicians to fight the war. French egalitarian effect.
lack of pictures in Bourbaki
lack of pictures in Bourbaki's work, and ties to religion, puritans, protestants, jews.
Grothendieck on Bourbaki
synonym of elitism, narrow-minded dogmatism, cult of canonical form, hermetism, castrating anti-spontaneity.
- Writing the Ultimate Mathematical Textbook: Nicolas Bourbaki's Éléments de mathématique, in Eleanor Robson et al (eds.) Handbook of the History of Mathematics, Oxford, Oxford University Press (2009), 585-587.
- https://www.tau.ac.il/~corry/publications/articles/Bourbaki%20-%20OHHM.html
Vladimir Arnold on Bourbaki
genuine mathematicians do not gang up, but the weak need gangs in order to survive
--Vladimir Arnold
Benoit Mandelbrot on Bourbaki
young daughter of the Bourkaki, Betty Bourkaki, on X. https://twitter.com/Betty_Bourbaki/
Spent about 3 hours reading about Bourbaki.
Nicolas Bourbaki is a influential math group, used to be mysterious. I didn't know much about the group until recent years, from Wikipedia.
- “MacTutor History of Mathematics Archive” written by J J O'Connor and E F Robertson, University of St Andrews.
- https://mathshistory.st-andrews.ac.uk/HistTopics/Bourbaki_1/
- https://mathshistory.st-andrews.ac.uk/HistTopics/Bourbaki_2/
Read also, Twenty-Five Years with Nicolas Bourbaki 1949–1973 (2008-07), by Armand Borel, from AMS Volume 45, Number 3. http://www.ams.org/notices/199803/borel.pdf
Some juicy quotes:
… Cartan was frequently bugging Weil with questions on how to present this material, so that at some point, to get it over with once and for all, Weil suggested they write themselves a new Traité d’Analyse. This suggestion was spread around, and soon a group of about ten mathematicians began to meet regularly to plan this treatise. It was soon decided that the work would be collective, without any acknowledgment of individual contributions. In summer 1935 the pen name Nicolas Bourbaki was chosen.
At this point let me simply mention that the true “founding fathers”, those who shaped Bourbaki and gave it much of their time and thoughts until they retired, are: Henri Cartan, Claude Chevalley, Jean Delsarte, Jean Dieudonné, André Weil.
born respectively in 1904, 1909, 1903, 1906, 1906— all former students at the École Normale Supérieure in Paris.
I was rather put off by the very dry style, without any concession to the reader, the apparent striving for the utmost generality, the inflexible system of internal references and the total absence of outside ones (except in Historical Notes).
LOL. I rather prefer this approach. Also, note some quotes from Wikipedia on criticism:
- # combinatorics is not discussed
- # logic is treated minimally[18]
Furthermore, Bourbaki make only limited use of pictures in their presentation.[19] In general, Bourbaki has been criticized for reducing geometry as a whole to abstract algebra and soft analysis.[20]
LOL. How dare they! I love combinatorics and logic and geometry.
also see:
Dieudonné at one point said “one can do nothing serious without them [Lie algebras]”, for which he was reproached.
This is typical arrogance from mathematicians. What a faaking bullshit. The Bourbaki books do not cover much of discrete math, for example, used in computer science. (computational math is too early in his time) But similar attitude you can often see in academic mathematicians today. The importance of discrete math, or computational math, is arguably a new era in math, overturning the traditional set theory based tower of foundations dealt by humans as treated in Bourbaki. See, for example: State of Theorem Proving Systems 2008, Notes on A New Kind of Science.