Harmonic Conjugacy

Definition: Harmonic Conjugacy

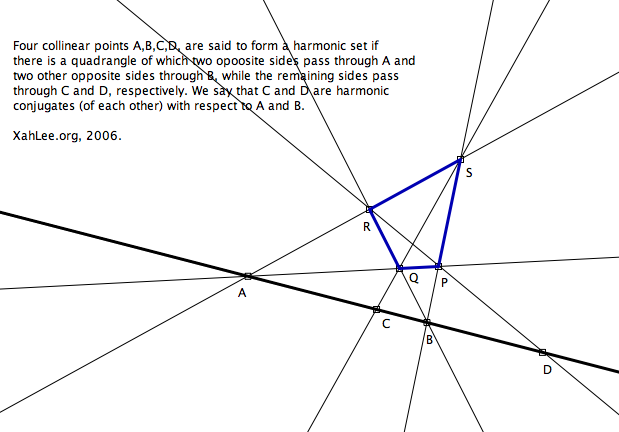
Four collinear points A,B,C,D, are said to form a harmonic set if there is a quadrangle of which two opposite sides pass through A and two other opposite sides through B, while the remaining sides pass through C and D, respectively. We say that C and D are harmonic conjugates (of each other) with respect to A and B, and we write H(AB,CD) as an abbreviated statement of this relation.

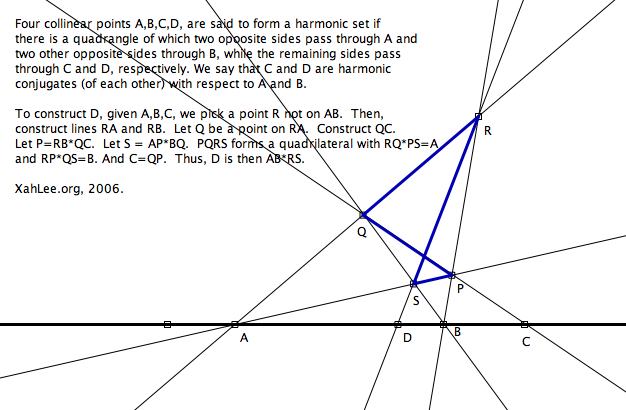
To construct D, given A,B,C, we pick a point R not on AB. Then, construct lines RA and RB. Let Q be a point on RA. Construct QC. Let P=RB*QC. Let S = AP*BQ. PQRS forms a quadrilateral with RQ*PS=A and RP*QS=B. And C=QP. Thus, D is then AB*RS.

Here's the phrasing from Coxeter:

We draw any triangle PQR whose sides QR, RP, PQ, pass through A,B,C, respectively. This determines a quadrangle PQRS, where S = AP*BQ. We thus obtain D = RS*AB. Of course we can also construct C given A,B,D by the same method.

Theorem

The harmonic conjugate of C with respect to A and B is independent of the choice of triangle PQR. Drag R or S and observe that points A,B,C,D forms a quadrangle (but not unique).

Proof:
Suppose that another such triangle P'Q'R' leads to a quadrangle P'Q'R'S'. We have to show that RS and R'S' both determine the same point D on AB. For this purpose we consider, in turn, three pairs of triangles. Corresponding sides of triangles PQR and P'Q'R' meet in the three collinear points A, B, C; hence, by Desargues's theorem, the joins of corresponding vertices are concurrent, that is, RR' passes through the point O = PP'*QQ'. Applying the same theorem to triangles PQS and P'Q'S', we conclude that SS' vertices of triangles RSP and R'S'P' all pass through O, and hence, by Desargues's theorem, their corresponding sides meet in collinear points; but two of these points are A and B; therefore, the remaining sides RS and R'S' both meet AB in the same point D.

Theorem

The sides of a quadrangle are divided harmonically by the sides of its diagonal triangle.

Proof: (Xah's outline) Suppose the quadrangle is P,Q,R,S, and its diagonal triangle vertexes is A,B,C. First we show that each side of the quadrangle are indeed cut into four parts. Pick any two point on the quadrangle, say {P,Q} that forms a line. One vertex of its diagonal triangle must be collinear with it, call it C. A triangle with one vertex C on a line PQ must necessary cut the line at one and only one more place, call it M. Therefore we have our four points P,Q,A,M. To show these points are a harmonic set, we need to find a quadrangle that defines them. The needed quadrangle are the remaining points not picked, in our case: R,S,A,B, and the pairs R,S and A,B will serve as the "remaining sides" that passes C and M respectively.

Definition: Harmonic Conjugacy
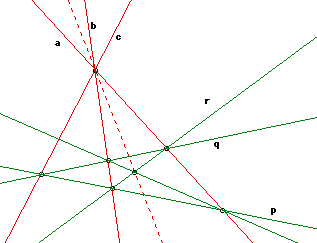
Four concurrent lines a,b,c,d, are said to form a harmonic set if there is a quadrilateral of which two opposite vertices lies on a and two other opposite vertices on b, while the remaining vertices lie on c and d. We say that c and d are harmonic conjugates (of each other) with respect to a and b, and we write H(ab,cd) as an abbreviated statement of this relation.

To construct d, given a,b,c, we draw any triangle pqr whose vertexes q*r, r*p, p*q, lie on a,b,c, respectively. This determines a quadrilateral pqrs, where s = (a*p)(b*q). We thus obtain d = (r*s)(a*b).