Deco-Cube

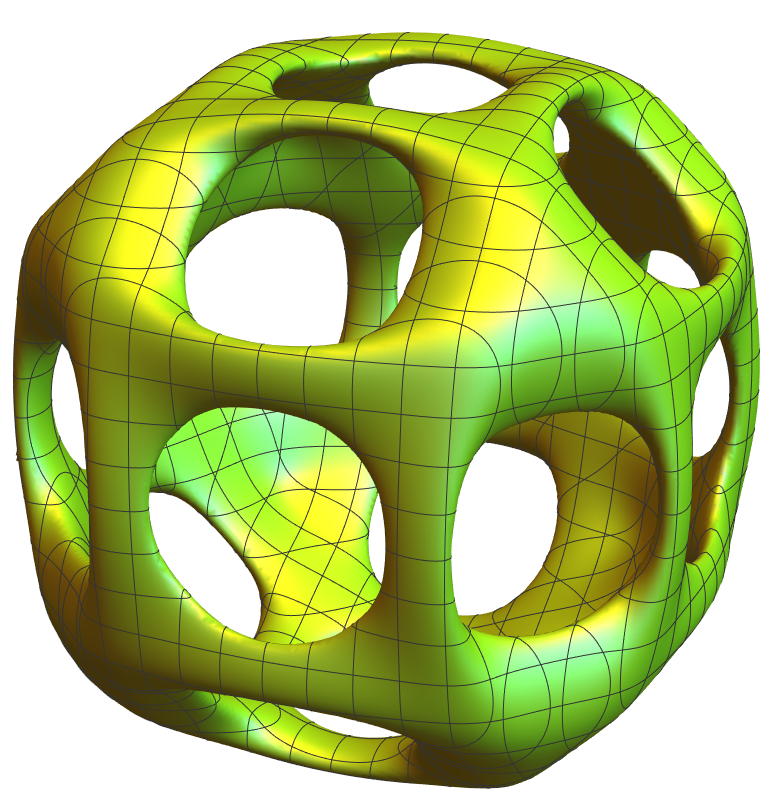
cc = 2.2; bb = 1; ff = 1.2; m = 2.5; ContourPlot3D[
   ((x^2 + y^2 - cc^2)^2 + (z - 1)^2*(z + 1)^2)*((y^2 + z^2 - cc^2)^2 +
       (x - 1)^2*(x + 1)^2)*((z^2 + x^2 - cc^2)^2 + (y - 1)^2*(y + 1)^2) -
     ff*(1 + bb*(x^2 + y^2 + z^2)) == 0, {x, -m, m}, {y, -m, m}, {z, -m, m},
   PlotRange -> All, PlotPoints -> 80, Axes -> False, Boxed -> False,
   ContourStyle -> Directive[RandomColor[], Opacity[1], Specularity[1, 20]]]

By manipulating several algebraic equation of torus, we can create equations of surfaces with a desired genus, also for the esthetic appeal. This surface is generated by arranging six circles positioned as the faces of a cube.