Helicoid-Catenoid

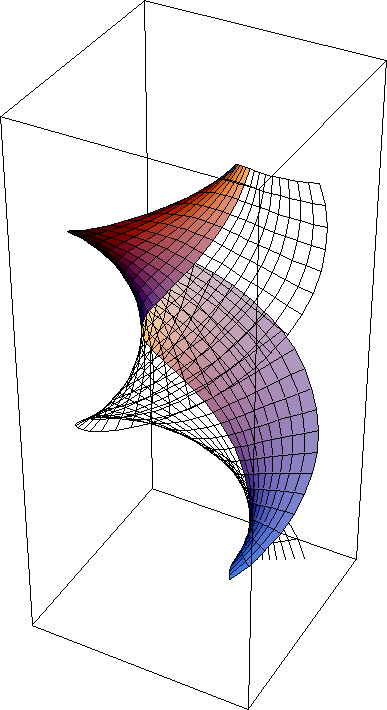
Helicoid-Catenoid is a family of Minimal Surfaces

Manipulate[ParametricPlot3D[
   {Cos[b]*Sinh[v]*Sin[u] + Sin[b]*Cosh[v]*
      Cos[u], (-Cos[b])*Sinh[v]*Cos[u] +
     Sin[b]*Cosh[v]*Sin[u], Cos[b]*u + Sin[b]*v},
   {u, 0, Pi*2}, {v, -1, 1}, PlotPoints ->
    {40, 20}], {b, 0, Pi/2}]

u controls the height of the surface. It has a period of 2*π. v controls the width of the surface. b is the parameter. If b=0, the surface is a helicoid. If b=π/2, the surface is a Catenoid. When b is 0, there is no “hole” along the axis. With b getting larger, the hole grows, and the flattness of the surface gets more curved. If v is very large, the surface looks like a sheet of paper, or stacks of sheets.

helicoid-catenoid.nb

Catenoid and Helicoid Isometry

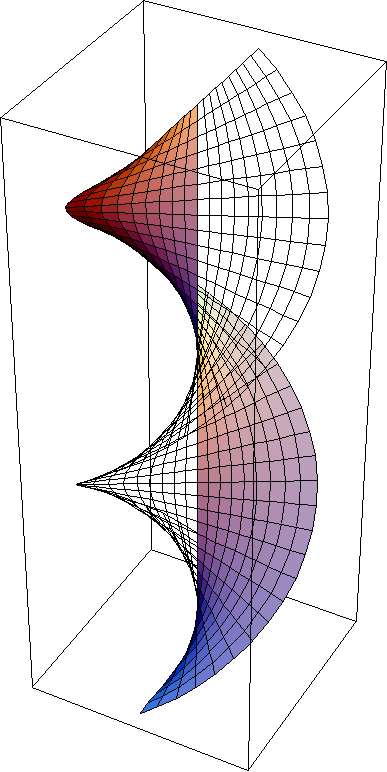
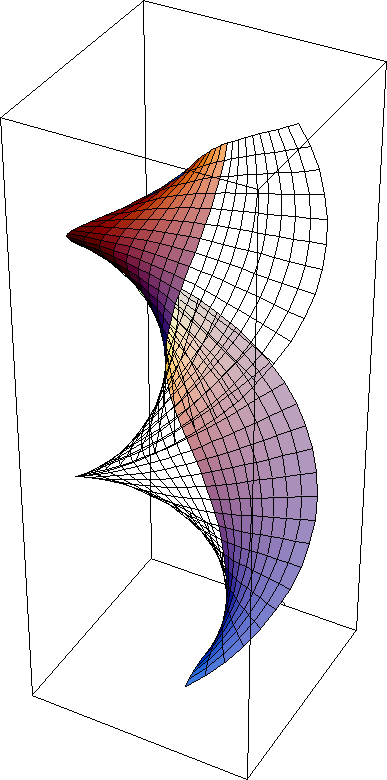
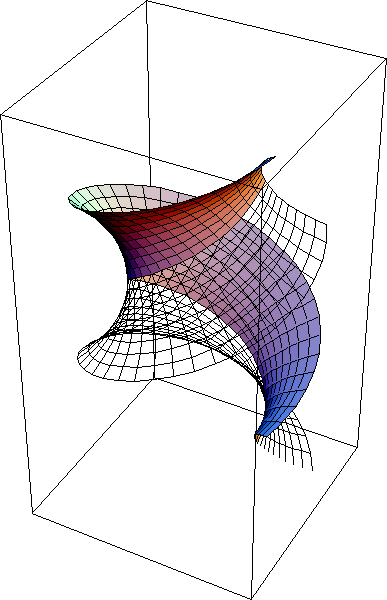
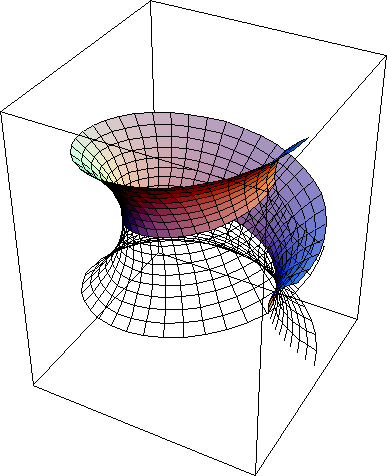
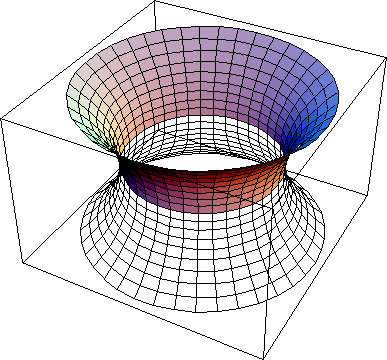
Helicoid and Catenoid are two surfaces having the same local geometry. This animation shows a continuous transformation between the two surfaces. Note that each and every surface in between are all minimal surfaces and isometric.

Explanation: suppose we draw a straight line (shortest path) between points A and B on a piece of paper. Now we slowly warp the paper into a cynlinder. We note, that the shortest path between the points A and B is still the line we drew on the surface. This tells us, that a cylinder and plane really are the same surface with respect to local geometry. That means, all distances and angles are not distinguishable between the two surfaces. Only when we consider the whole suface and their topology, then are a plane and cylinder different. In other words, a two-dimensional being (ant) living on the surface wouldn't be able to tell the shape of their 2-dimensional space by any measures of distances or angles. To them, a plane and a cylinder (or arched plane) are indisquishable. When two surfaces having this property, we say that their local geometries are identical, or that they are locally isometric. The local isometry of cylinder and a plane is a trivial example. The helicoid-catenoid family of surfaces is a non-trivial example. They are all locally isometric, and they are all minimal surfaces.

For a video, see: http://VirtualMathMuseum.org/Surface/helicoid-catenoid/helicoid-catenoid.html