Catenary

History
From Robert Yates:
Galileo was the first to investigate the catenary which he mistook for parabola. James Bernoulli in 1691 obtained its true form and gave some of its properties.
From E H Lockwood A book of Curves (1961):
Galileo's suggestion that a heavy rope would hang in the shape of a parabola was disproved by Jungius in 1669, but the true shape of the “chain-curve”, the catenary, was not found until 1690/91, when Huygens, Leibniz and John Bernoulli replied to a challenge by James Bernoulli. David Gregory, the Oxford professor, wrote a comprehensive treatise on the “catenarian” in 1697. The name was first used by Huygens in a letter to Leibniz in 1690.
Description
Catenary (also known as chainette, alysoid, and hyperbolic cosine) is defined as the curve of the function Cosh[x].
Cosh[x]
is defined as
(E^x + E^(-x))/2
.
The capital E denotes the natural logarithm base constant often denoted by a lower case e.
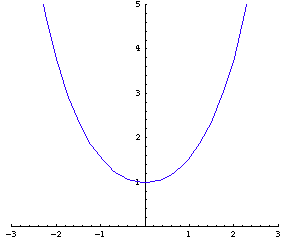
Catenary is the shape of a ideal string hanging from two points. By “ideal” it is roughly meant that the string is perferctly flexible, inextensible, no thickness, of uniform density, and possibly other attributes. In other words, catenary is the mathematical abstraction of the shape of hanging strings. We can say that catenary approximates the shapes of most hanging string-like objects we see. These include ropes, outdoor telecommunication wires, necklaces, chains…etc. in terms of pure math, what is the problem that that Cosh[x] is a solution to?
It is worthwhile to note that catenary has only one shape (it is not a family of curves). If you hold the two ends of a string, and vary the distance of their endings, you will see shapes of different sharpness and wonder how can they all be catenary. In fact, you are merely seeing different scales of catenary. The phenomenon is the same as looking at part of a circle. The closer you look, the straighter it is but the whole circle never changes shape. At each instance you are holding the string, the law of physics dictates its shape to be part of the catenary (since the string is finite in length). The wider apart the endings, the smaller part of catenary you see. It is also a common misunderstanding to assume parabolas as a curve of many shapes.
Formula
Parametric: {t, Cosh[t]}.
Properties
Caustic of expontial curve
The Catacaustic of the Exponential Curve with light rays from above and parallel to the y axes is the catenary. prove that catacaustic of E^x is Cosh[x]
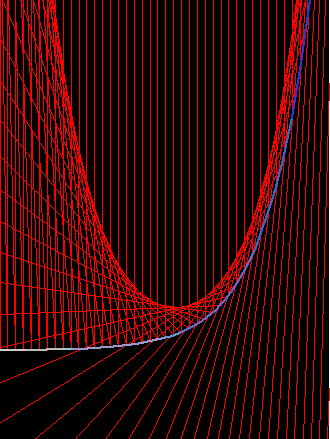
The exponential curve E^x has the interesting property itself. It is the only function whose derivative is itself.
Involute
The involute of catenary starting at the vertex is the tractrix. prove that involute of Cosh[x] is tractrix.
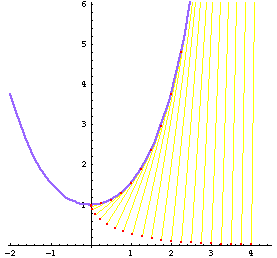
Radial and Kampyle of Eudoxus
The radial of catenary is the Kampyle of Eudoxus. In the figure blow, the blue curve is half of catenary. The green curve is Kampyle of Eudoxus {-Cosh[t]*Sinh[t],Cosh[t]}. The rainbow lines are the radiuses of osculating circles. J D Lawrence says that the evolute of catenary is also the tractrix. prove it.
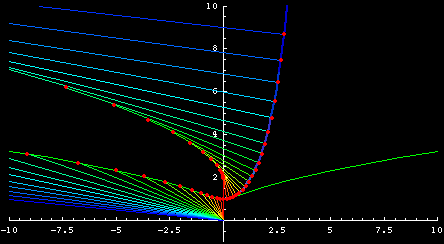
surface of revolution and catenoid
A catenary rotating around a axis forms the catenoid, which is a mimimum surface.
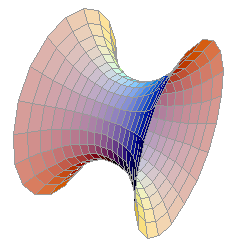
Minimum surface are surfaces that connect given curves in space and has the least area. That is one simple way to define minimal surfaces. Catenoid is the minimum surface between two parallel circles on a cylinder or circular cone. You can see minimal surfaces in nature as soap films. Bend wires into two parallel circles and dip them into soap solution. The soap film between the two circles is the catenoid. (catenoid_plot.nb)
Photos



It is claimed in publications that Suspension bridge has the form of parabolas… See http://whistleralley.com/hanging/hanging.htm.