Xah Talk Show 2024-08-14 Ep574, Advent of Code 2023, Day 12, Wolfram Language

- 02:36:39 summary
toy input
???.### 1,1,3 .??..??...?##. 1,1,3 ?#?#?#?#?#?#?#? 1,3,1,6 ????.#...#... 4,1,1 ????.######..#####. 1,6,5 ?###???????? 3,2,1
solution for toy problem is
???.### 1,1,3 - 1 arrangement .??..??...?##. 1,1,3 - 4 arrangements ?#?#?#?#?#?#?#? 1,3,1,6 - 1 arrangement ????.#...#... 4,1,1 - 1 arrangement ????.######..#####. 1,6,5 - 4 arrangements ?###???????? 3,2,1 - 10 arrangements
total is 21
- possible case
- ??????????????????????????????????????????????????? 2
- 51 question marks.
- this would become exponential time if brute force.
(exp 8) ;; e^8 (expt 2 8) (expt 2 10) ;; 1024 (#o2000, #x400) (expt 2 51) ;; 2 251 799 813 685 248
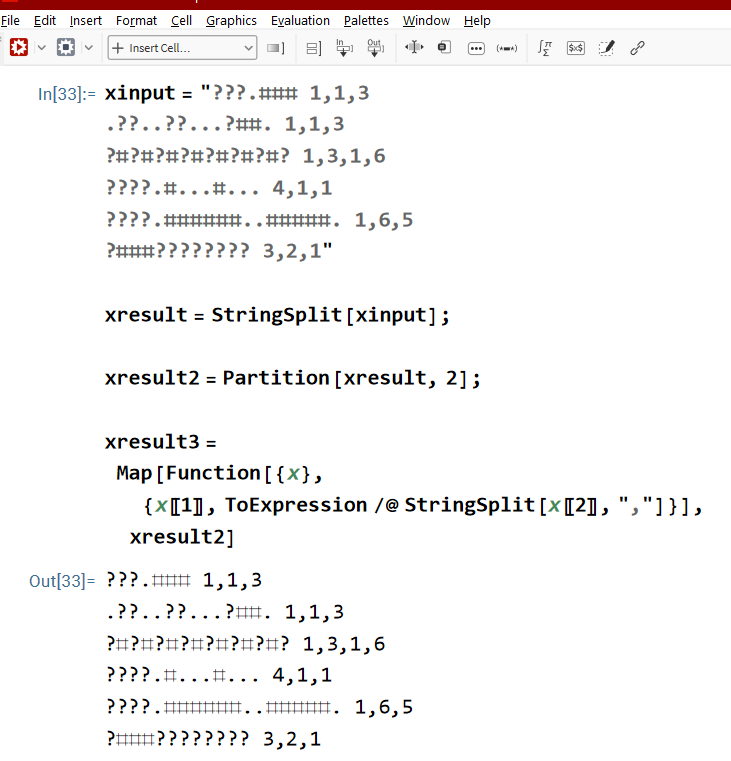
xinput = "???.### 1,1,3 .??..??...?##. 1,1,3 ?#?#?#?#?#?#?#? 1,3,1,6 ????.#...#... 4,1,1 ????.######..#####. 1,6,5 ?###???????? 3,2,1" xresult = StringSplit[ xinput ]; xresult2 = Partition[ xresult , 2] ; xresult3 = Map[ Function[{x}, {x[[1]], ToExpression /@ StringSplit[ x[[2]], "," ]} ], xresult2 ] Print @ xresult3 (* some description. for each line, there are 2 parts. on the left side is, the STRING MASK. on the right side is, GROUPING NUMBERS. the length of GROUPING NUMBERS is lets say g. you need to find all possible solutions. actually, just a count of them. ------------------ algorithm: exploration. take the string, and split by dots. count the length of the list. lets say tg. it's a tentative grouping number. now, compare tg with g. If equal, basically no need to split further. If lesser, means, some of the question mark string sequence needs to be split. diff = g - tg diff, is the number of places you need to replace question by dot. and, they cannot not be consecutive. you can split, only if, the question mark is not on the edge of the group. If greater, some of the consecutive question mark needs all be replaced by dots. exactly which group we can eliminate, depends on the grouping numbers. ------------------ simply brute force, replace all possible replacement of question mark by dot, and check if it works. the most brute force way, is to count number of question marks in the string mask, say it's n , then, you have 2^n ways. find all the possible binary sequence, as a list binary-seq-list. then, map a function to the binary-seq-list, each time, replace ? by # if it's 1, else replace by dot. then, split the result string by dot, count # for each group, and see if it matches the grouping number. advent of code 2023, day 12 --------------------- new approach. simply, for each line, e.g. {???.###,{1,1,3}} consider the length of the string mask on the left. 7. then, the sequence of grouping numbers 1 1 3. length is 3. so, consider binary number of 7 digits. compute possible grouping of 1s in this binary number. then, consider such groupings of 1 1 3. but then, minus, given mask. *)