Circle (in the works)
Description
A circle is a curve such that there is a point C such that the distance from C to any point P on the curve is constant. This point C is called the center of the circle, and the constant distance[C,P] is called the circle's radius.
The polar equation for circle is easily r==C, where C is a constant. The equation for Cartesian coordinate is also easily derived. The distance from two points {x,y} and {c1,c2} is Sqrt[(x-c1)^2 + (y-c2)^2] by the Pythagorean theorem. set this to a constant r, and let x and y be variable, then we have the Cartesian equation Sqrt[(x-c1)^2 + (y-c2)^2] == r
History
Formula
Polar formula: r == b, where b is a constant.
Cartesian equation Sqrt[(x-c1)^2 + (y-c2)^2] == b, where b is the constant and {c1,c2} is the center.
Parametric: t*{Cos[t],Sin[t]}, t goes from 0 to 2 Pi.
Properties
Circles are so fundamental in mathematics that it plays a basic role in almost every branch of geometry or analysis. The following lists some of the geometric properties or notable facts about circles.
Constant Curvature
By definition, the curvature of a circle is constant everywhere. And, it is simply 1/r, where r is the radius of the circle. So, if the circle is large, its curvature 1/r is small. If the circle is small, 1/r is then large, so the curve is more curved. In extreme cases, if r is 0, we have a circle so small that it is a dot, and its curvature 1/r is infinitly large. Likewise, if r is infinity, the circe is so large that its curvature 1/r is 0, like a line.
Thales's Theorem
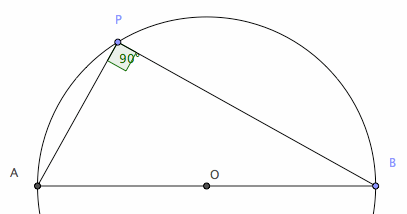
Theorem: Let A and B opposite points on a circle. Let P be a point on a circle. Angle[A,P,B] is a right angle.
Proof: Let O be the circle's center. Let a be the value of angle[O,A,P]. Let b be the value of angle[P,B,O]. Let p be the value of angle[A,P,B]. We want to show that p==Pi/2. Since the angles of a triangle adds to Pi, we have: a + b + p == Pi. Also, note that dist[O,A]==dist[O,P], therefore triangle[A,O,P] is an isosceles triangle, thus angle[A,P,O]==a. Similar argument to the triangle[O,P,B] gets us: angle[O,P,B] == b. Since angle p is the sum of angle APO and OPB, thus we have p = a + b. Combined this equation with a + b + p == Pi, we get p == Pi/2. End of Proof.
Converse of Thales's Theorem
Theorem: Let there be a right triangle. Let a circle passes thru the 3 vertexes of the triangle. The longest side of the triangle is a diameter of the circle.
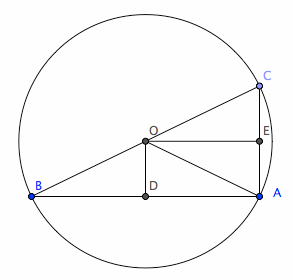
Proof: Let A, B, C be the 3 vertexes of a right triangle, and BC its longest side. Let O be the midpoint of BC. Let D be a line passing O and perpendicular to AB.
It is given that CBA is a right triangle. By construction, CBD is also a right triangle. Because CBA and CBD share the angle at B and are both right triangles, therefore the corresponding side's lengths of the triangles are proportional to a factor. Since O is the midpoint of AC, therefore length BO is half of BC. Further, D is the midpoint of BA. Triangle OBD and ODA both share the right angle at D, and share the side OD, and the distance[B,D]==distance[D,A], therefore the two triangles are congruent, and distance[O,B]==distance[O,A].
Now, using the same argument above, apply the same construction of passing a line thru O and perpendicular to AC, we derive that distance[O,C]==distance[O,A]. Since now distance[O,C]==distance[O,A]==distance[O,B], therefore O is the center of a circle passing ABC.
Archimedes's Circle
Theorem: Let there be a fixed circle and a fixed point O in the plane. Let P and Q be the intersections of the circle and a line passing O. distance[O,P]*distance[O,Q] is a constant.
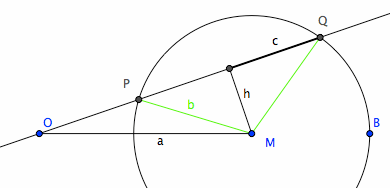
Proof: Let the center of the circle denoted by M, and radius be b. Let the distance[O,M] be a.
The triangle[P,M,Q] is a isosceles and O is a point on the line PQ. Let H be the midpoint of PQ. Let h denote distance[M,H] and c denote distance[P,Q]/2. distance[O,P] and distance[O,Q] can be now represented by (OH+c) and (OH-c) if O is outside of PQ, or (OH+c) and (c-OH) if O is inside of PQ. And their product is either (OH^2 - c^2) or (c^2 -OH^2).
Now, OHM is a right triangle with OM := a, so we have OH^2 == a^2-h^2. Similarly, c^2 == b^2 - h^2. Substitute OH^2 and c^2 in the last expression and simplify we have a^2-b^2 if O is outside of PQ, or (b^2-a^2) if O is inside of PQ. Both of which is a constant. If O coincides with P or Q then OP*OQ == 0. End of Proof.
Circle defined by Three points
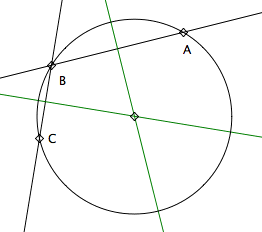
Given 3 non-linear points, there is a unique circle passing through them. The center of the circle is the intersection of two bisectors of any two given point. If the 3 points lies on a line, then the “circle” passing them will be a line. This is another point of view that lines can be considered as circles with infinite radius.
Similarly, given a circle and a point not on the plane of the circle, a sphere is defined. Alternatively, a sphere is defined with 4 points in space not all co-planar. The proof can be easily constructed by considering cross-sections as the planar case, and locate the sphere's center by bisection.
Geometric Inversion and Relation to Lines
A circle is used to define geometric inversion. In this way, a line can be considered as a circle with infinite radius, and reflection over a line is just a special case of geometric inversion.
Conic Sections
Pole and Polars
Ratio of Circumference and Diameter
The ratio of the circumference of a circle and its diameter is a constant, called pi, and has the value approximate to 3.141592. Pi is a irrational number. Pi is one of the most important constant in mathematics. The study of pi spawned vast number of branches of mathematics since the very beginning of math's history.
Circular Functions
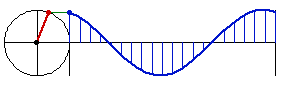
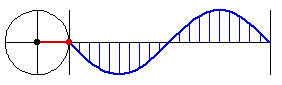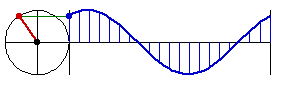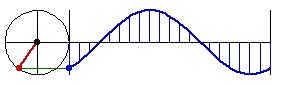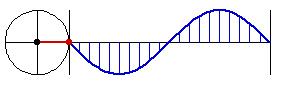
A circle is the essence of the trig function sine. The trig functions: Sin, Cos, Tan, Sec, Cos, Cot are all based on a single function Sin. The essence of the sine function is that we want a smooth function that oscillates, as to form a wave. The natural development of this idea, is to base on a point moving on circle in constant speed, and record its height with respect to time. This is why, the function sine is sometimes called circular function.
Steiner Circles
See p.184, p.136 of Visual Complex Analysis
Apollonian Circles
Circle and Triangles
Related Web Sites
See: Websites on Plane Curves, Plane Curves Books .
Robert Yates: Curves and Their Properties .
Equation of a Circle from 3 Points By Paul Bourke. http://local.wasp.uwa.edu.au/~pbourke/geometry/circlefrom3/