Hyperbolic Trig Functions (in the works)
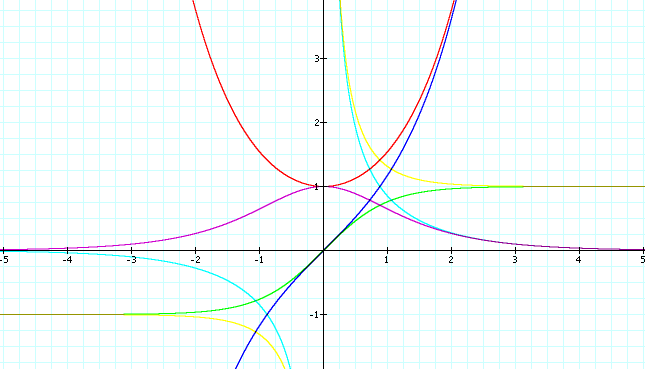
Description
Sinh is called Hyperbolic Sine. Sinh and 5 other functions are analogous to the trig functions. They are defined this way:
Sinh[x]:= ( E^2-E^(-x) )/2or-I*Sin[I*x]Cosh[x]:= ( E^2+E^(-x) )/2orCos[I*x]Tanh[x]:= Sinh[x]/Cosh[x]or-I*Tan[I*x]Sech[x]:= 1/Cosh[x]Csch[x]:= 1/Sinh[x]Coth[x]:= Cosh[x]/Sinh[x]
The E is the number
Limit[(1 + 1/x)^x, x -> Infinity]
~= 2.71828. The capital I denotes the complex number
Sqrt[-1]
.
They are called hyperbolic trig functions because they bear strong similarities to the trig functions. Trig functions relate to a circle, while hyperbolic trig functions relate to a rectangular hyperbola x^-y^==1 in a similar way. And all identies of trig functions have a analogue in the hyperbolic ones of the same form.
The hyperbolic cosine Cosh is famously known as catenary .