Hyperbola

Clear[xc,xaalist,xcount] xc = 1; xcount = 7; xaalist = Table[x, {x, .25, .99, (.99 - .25)/xcount}]; ParametricPlot[ Evaluate@ Table[{a Sec[t], Sqrt[xc^2 - a^2] Tan[t]}, {a, xaalist}], {t, 0.01, 2 Pi - 0.01}, PlotStyle -> Map[Function[{Thickness[.01], #1}] , Table[Hue[0, i, 1], {i, .3, 1, (1 - .3)/xcount}]], PlotRange -> {{-1, 1}, {-1, 1}} 3 xc, Background -> Hue[0.18], (* PlotLabels -> xaalist, *) PlotLabels -> Placed[ xaalist, Left ], AspectRatio -> Automatic, Prolog -> {{Hue[.75], PointSize[.03], Point[{-1, 0}], Point[{1, 0}]}}]

Clear[ xhformula, xelist, xhypers ] xhformula[e_] := Function[{Sec[#], Sqrt[e^2-1] Tan[#]}] ; (* a Sqrt[ e^2-1] == b *) (* e = c/a for all conics *) xelist = Table[ 1/x, {x,.25,.99, (.99-.25)/7}] xhypers = Table[ xhformula[x][t], {x, xelist}] ParametricPlot[ Evaluate@ xhypers , {t, 0.01, 2 Pi -0.001 }, AspectRatio->Automatic, PlotRange->{{-5,5},{-5,5}}, PlotStyle-> Map[ Function[{Thickness[.01],#1}], Table[Hue[.75,i,1],{i,.3,1,(1-.3)/7}]], Background->Hue[.18], Axes->False ]
History
Description
Hyperbola describe a family of curves with single parameter. Together with ellipse and parabola, they make up the conic sections .
Hyperbola is commonly defined as the locus of points P such that the difference of the distances from P to two fixed points F1, F2 (called foci) are constant. That is, Abs[ distance[P,F1] - distance[P,F2] ] == 2 a, where a is a constant. GeoGebra: Two Ripples Traces Conics .
The eccentricity is a number that describe the “flatness” of the hyperbola. Let the distance between foci be 2 c, then eccentricity e is defined by e := c/a, and 1 < e. The larger the eccentricity, the more it resembles two parallel lines. As e approaches 1, the vertexes become more pointed.
The line passing through foci is the axis of the hyperbola. A line passing through center and perpendicular to the axis is the transverse axis. The vertexes are the intersections of the hyperbola and its axis.
Formula
- vertexes at {-1,0} and {1,0}
- eccentricity e
- (foci is {-e, 0} and {e, 0})
Parametric equation
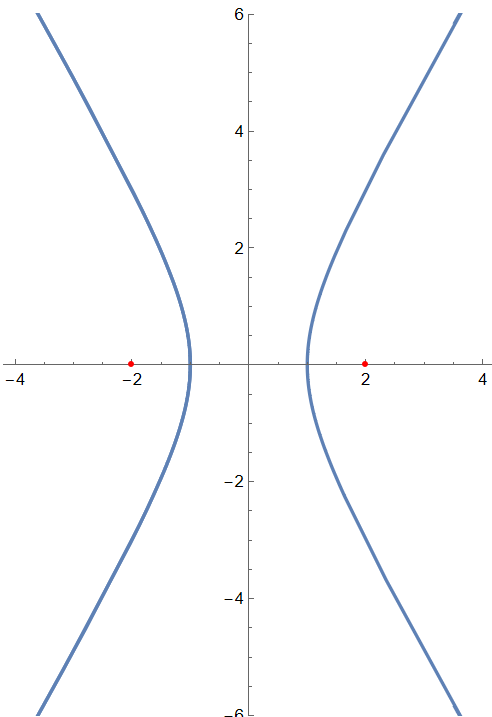
Clear[xecc] xecc = 2; ParametricPlot[{Sec[t], Sqrt[e^2 - 1] Tan[t]}, {t, -5, 5}, PlotRange -> {{-1,1} 5, {-1,1} 6} , Epilog -> {Red, Point[ {-xecc,0} ], Point[ {xecc,0} ]} ]
Cartesian equation
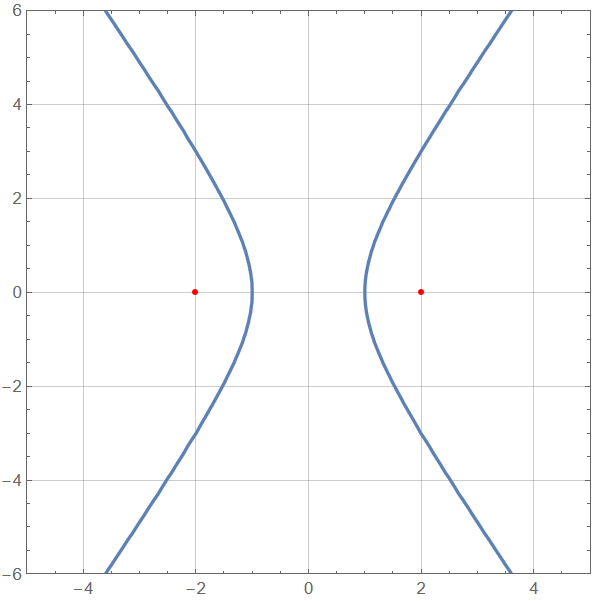
Clear[ xecc ] xecc = 2; ContourPlot[ x^2 - y^2/(xecc^2-1) == 1 , {x, -5, 5}, {y, -6, 6}, PlotRange -> {{-1,1} 5, {-1,1} 6} , GridLines -> Automatic, Epilog -> {Red, Point[ {-xecc,0} ], Point[ {xecc,0} ]} ]
- vertex at {-a,0}, {a,0}
- directrix at
x == -a/e,x == a/e - asymptotes at
y== -b/a x,y== b/a x
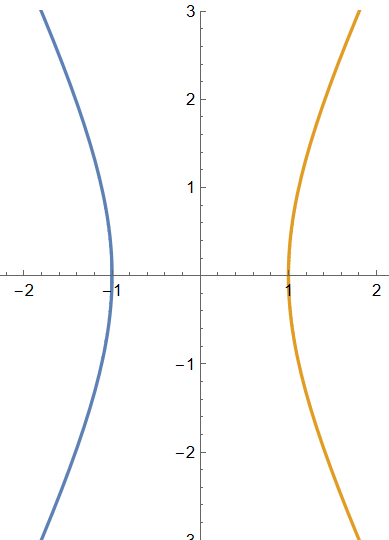
Clear[ xa,xb ] xa = 1; xb = 2; ParametricPlot[ Evaluate[ {{-xa Cosh[t], xb Sinh[t] }, {xa Cosh[t], xb Sinh[t] }} ] , { t, -2, 2}, PlotRange -> {-3,3} ]
Cartesian equation

Clear[aa, bb] aa = 1; bb = 2; ContourPlot[x^2/aa^2 - y^2/bb^2 == 1, {x, -5, 5}, {y, -5, 5}, GridLines -> Automatic]
The parametric form with Sinh is derived by replacing y in x^2/a^2-y^2/b^2==1 with b*Sinh[t], then solve for x. This is analogous to the ellipse case where we replace a variable in x^2/a^2+y^2/b^2==1 by Cos[t] and solve the other to find {a*Cos[t],b*Sin[t]}.
Rectangular Hyperbola
- A rectangular hyperbola is a hyperbola with eccentricity Sqrt[2] ≈ 1.4142.
- Its asymptotes are mutually perpendicular.
- A simple Cartesian equation for rectangular hyperbola is
x y == 1
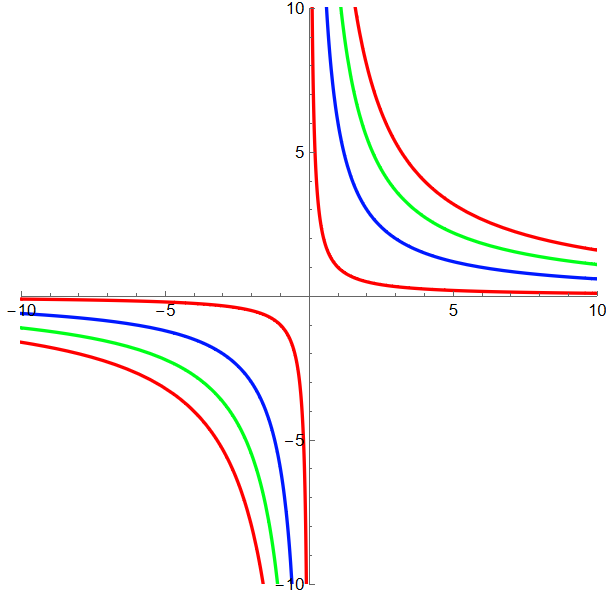
ParametricPlot[Evaluate@ Table[{t, i/t}, {i, 1, 20, 5}], {t, -10, 10}, PlotStyle -> {Hue[0], Hue[.65], Hue[.35]}, PlotRange -> {{-1, 1}, {-1, 1}} 10, AspectRatio -> Automatic]
- Rectangular hyperbola have the property that when streched along one or both of its asymptotes, the curve remains the same.
- That is, the curve {t, 1/t n}, {t n, 1/t}, and {t, 1/t} Sqrt[n] are the same curve with various degrees of magnification.
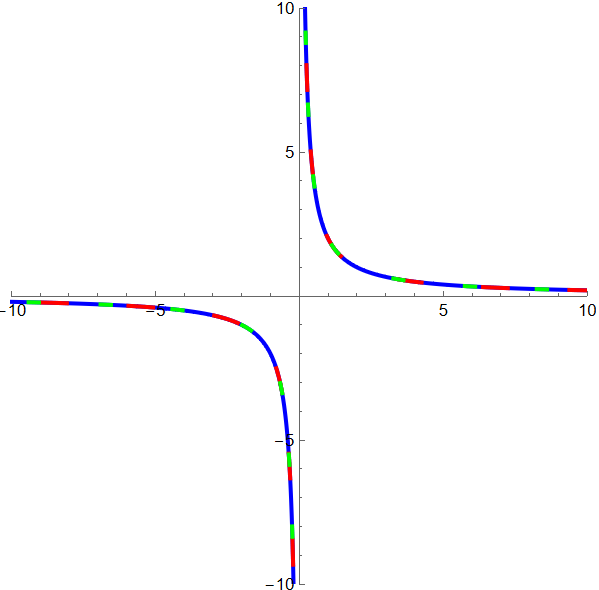
(* plotting 3 curves, with different colored dash lines, showing they overlap *) Clear[n]; n = 2; ParametricPlot[ { {t, n 1/t}, {n t, 1/t}, {t, 1/t} Sqrt[n]}, {t,-12,12}, PlotStyle->{ {Blue, Thickness[.007]}, {Red, Thickness[.007], Dashing[{.05,.1}]}, {Green, Thickness[.007], Dashing[{.025,.1}]} }, PlotRange->{{-1,1}, {-1,1}} 10, AspectRatio->Automatic ]
Point-wise construction
This method is derived from the paramteric formula for hyperbola
{a Sec[t], b Tan[t]}
, where a and b are the radiuses of the concentric circles.
If a == b , then the curve traced is rectangular hyperbola.
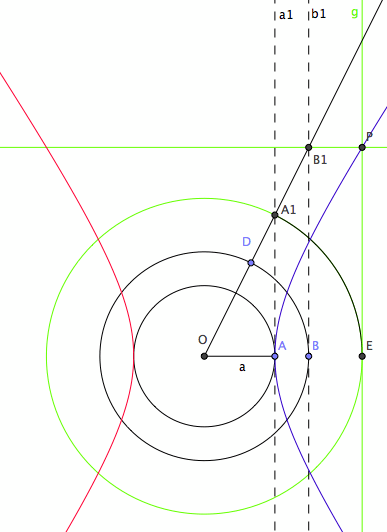
- Let O be the origin. Let A and B be points on the positive x-axis.
- Let there be a circle centered on O and passing A.
- Let there be a circle centered on O and passing B.
- Let there be a line a1, that passes A and parallel to y-axis.
- Let there be a line b1, that passes B and parallel to y-axis.
- Let there be a point D on one of the circle.
- Let there be a line OD.
- Let A1 := Intersection[Line[O,D],a1]
- Let B1 := Intersection[Line[O,D],b1]
- Let there be a circle centered on O passing A1. Let the intersection of this circle and positive x-axis be E. Let there be a line g, passing E and parallel to y-axis.
- Let there be a line passing B1 and parallel to x-axis.
- The locus of intersection g and B1, as D moves on the circle, is a hyperbola.
Needs["PlaneCurveGenerator`"] ListAnimate@ HyperbolaGenerator[{2, 1}, {0, 1.25}, PlotRange -> {{-2, 7}, {-2, 6}}, Ticks -> {Range[-10, 10, 2], Range[-10, 10, 2]}]
Optical Property
Light rays coming from one focus of a hyperbola refract to the other focus.

Needs["PlaneCurvePlot`"] PlaneCurvePlot[{-Sec[t], Tan[t]}, {t, 0, 2 Pi, 2 Pi/50}, CausticLineLength -> 30, CausticOrigin -> {Sqrt[2], 0}, PlotDot -> False, PlotRange -> {{-4, 4}, {-4, 4}}, CausticLineStyle -> Table[Hue[i], {i, 0, 1, 1/50}], Epilog -> {Red, Disk[{-Sqrt[2], 0}, 0.1]}, Background -> Black]
Pedal
The pedal of a hyperbola with respect to a focus is a circle.
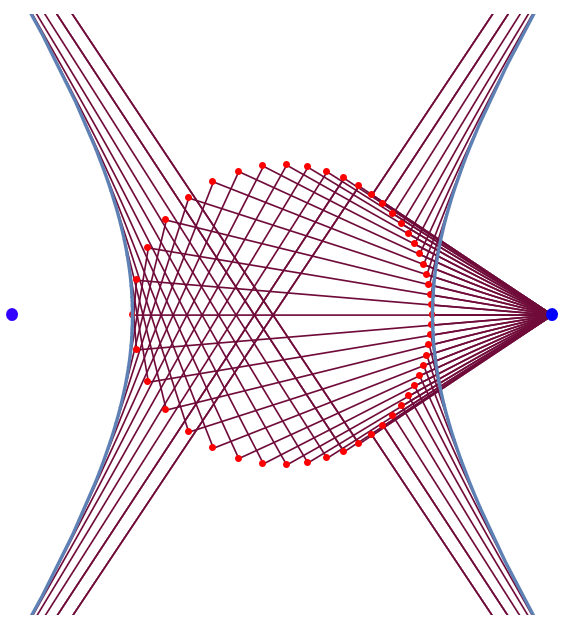
Needs[ "PlaneCurvePlot`" ] Clear[ecc, Hyperbola]; ecc = 1.8; Hyperbola[ecc_] := Function[{-Sec[#], Sqrt[ecc^2-1] Tan[#]} ] (* a Sqrt[ ecc^2-1] == b *) (* ecc = c/a for all conics *) PlaneCurvePlot[ Hyperbola[ecc][t], {t, -Pi , Pi , (2 Pi )/50}, PedalPoint->{ecc,0}, PlotDot->False, PlotCurve->False, LineStyle->{RandomColor[ ]}, AspectRatio->Automatic, Axes->False, PlotRange->{{-1,1},{-1,1}} 2, Epilog->{ {Hue[.7], PointSize[.02], Point[{-ecc,0}]} } ]
The pedal of a rectangular hyperbola with respect to its center is a lemniscate of Bernoulli
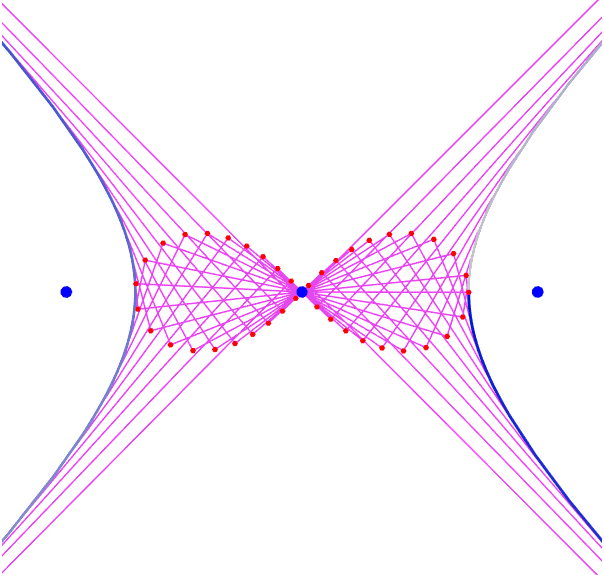
Needs[ "PlaneCurvePlot`" ] Clear[e, Hyperbola]; e = Sqrt[2]; Hyperbola[ecc_] := Function[{-Sec[#], Sqrt[ecc^2-1] Tan[#]} ] PlaneCurvePlot[ Hyperbola[e][t], {t, -3.14,3.14, 6.18/40}, PedalPoint->{0,0}, PlotDot->False, LineStyle->RandomColor[], AspectRatio->Automatic, Axes->False, PlotRange->{{-1,1},{-1,1}} 1.8, Epilog->{ {Blue, PointSize[.02], Point[{-e,0}], Point[{e,0}]} } ]
Inversion
The inversion of a rectangular hyperbola with respect to its center is a lemniscate of Bernoulli.
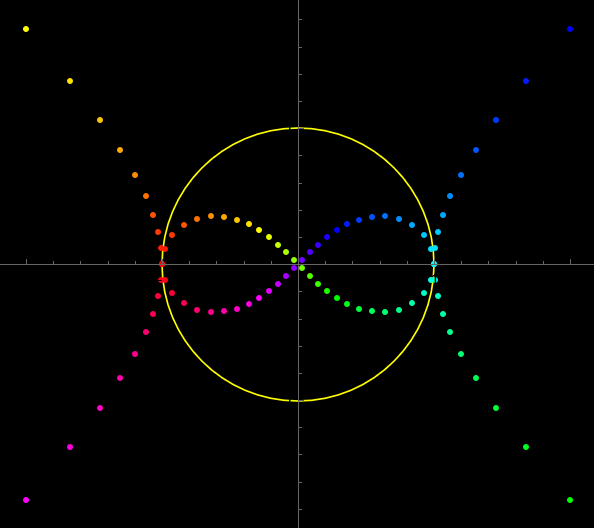
Needs["PlaneCurvePlot`"] Clear[ecc, Hyperbola]; ecc = Sqrt[2]; Hyperbola[ecc_] := Function[{-Sec[#], Sqrt[ecc^2 - 1] Tan[#]}] PlaneCurvePlot[Hyperbola[Sqrt[2]][t], {t, 0, 2 Pi, 2 Pi/54}, InversionCircle -> {{0, 0}, 1}, PlotCurve -> False, DotStyle -> Table[Hue[tt], {tt, 0, 1, 1/54}], PlotRange -> {{-1, 1}, {-1, 1}} 2.2, AspectRatio -> Automatic, Background -> Black ]
The inversion of a rectangular hyperbola with respect to a vertex is a right strophoid.
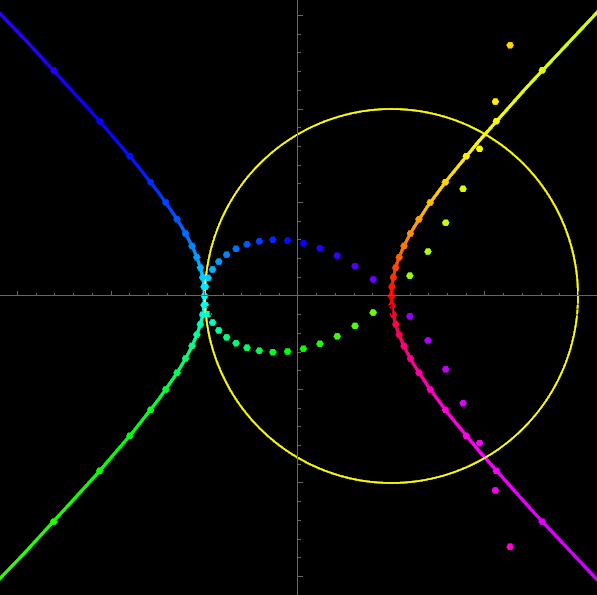
(*Inversion of rectangular hyperbola at the vertex*) Needs["PlaneCurvePlot`"] Clear[ecc, Hyperbola]; ecc = Sqrt[2]; Hyperbola[ecc_] := Function[{-Sec[#], Sqrt[ecc^2 - 1] Tan[#]}] PlaneCurvePlot[Hyperbola[ecc][t], {t, -Pi, Pi, 2 Pi/(4 16)}, InversionCircle -> {{1, 0}, 2}, PlotDot -> True, PlotCurve -> True, CurveColorFunction -> Hue, PlotRange -> {{-1, 1}, {-1, 1}} 3.2, DotStyle -> Table[{Hue[tt], PointSize[0.012]}, {tt, 0, 1, 1/(4 16)}], Background -> Black, AspectRatio -> Automatic]
The inversion of any hyperbola with respect to a focus is a limacon of Pascal .
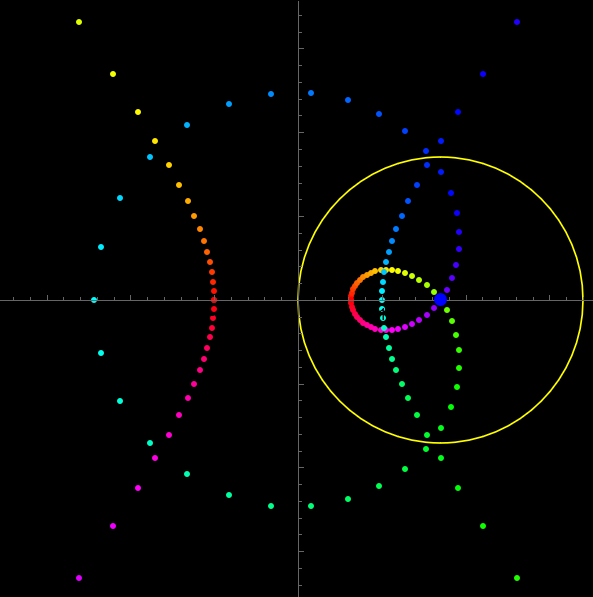
Needs["PlaneCurvePlot`"] Clear[ecc, Hyperbola] Hyperbola[ecc_] := Function[{-Sec[#], Sqrt[ecc^2 - 1] Tan[#]}] ecc = 1.7; PlaneCurvePlot[Hyperbola[ecc][t], {t, 0, 2 Pi, 2 Pi/80}, InversionCircle -> {{ecc, 0}, ecc}, PlotCurve -> False, DotStyle -> Table[Hue[tt], {tt, 0, 1, 1/80}], AspectRatio -> Automatic, PlotRange -> {{-1, 1}, {-1, 1}} 2.1 ecc, Epilog -> {Blue, PointSize[.02], Point[{ecc, 0}]} , Background -> Black]
Quadric Surfaces
Equations of polynomials of degree 2 with 2 variables have cross sections that are hyperbola, ellipse, parabola in various ways.
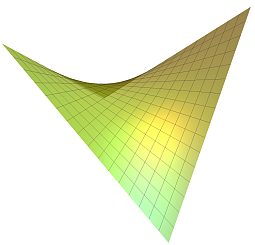 Hyperbolic Paraboloid
Hyperbolic Paraboloid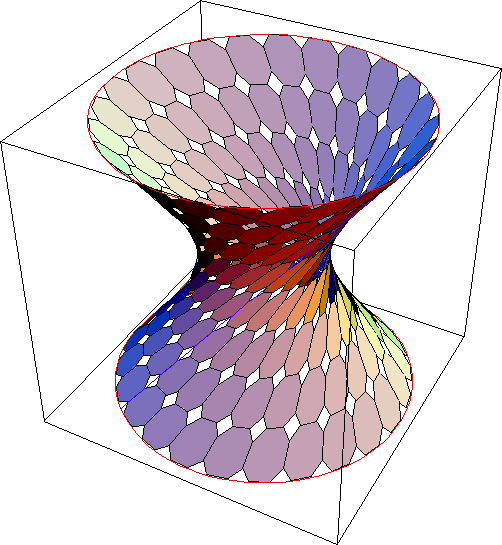 Hyperboloid of One Sheet
Hyperboloid of One Sheet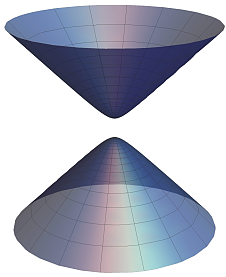 Hyperboloid of Two Sheet
Hyperboloid of Two Sheet