WolframLang vs Lisp Syntax

WolframLang syntax and lisp syntax are isomorphic. WolframLang syntax has this form in general: e0[e1, e2, e3] while lisp is (e0 e1 e2 e3)

Symbolic Expression

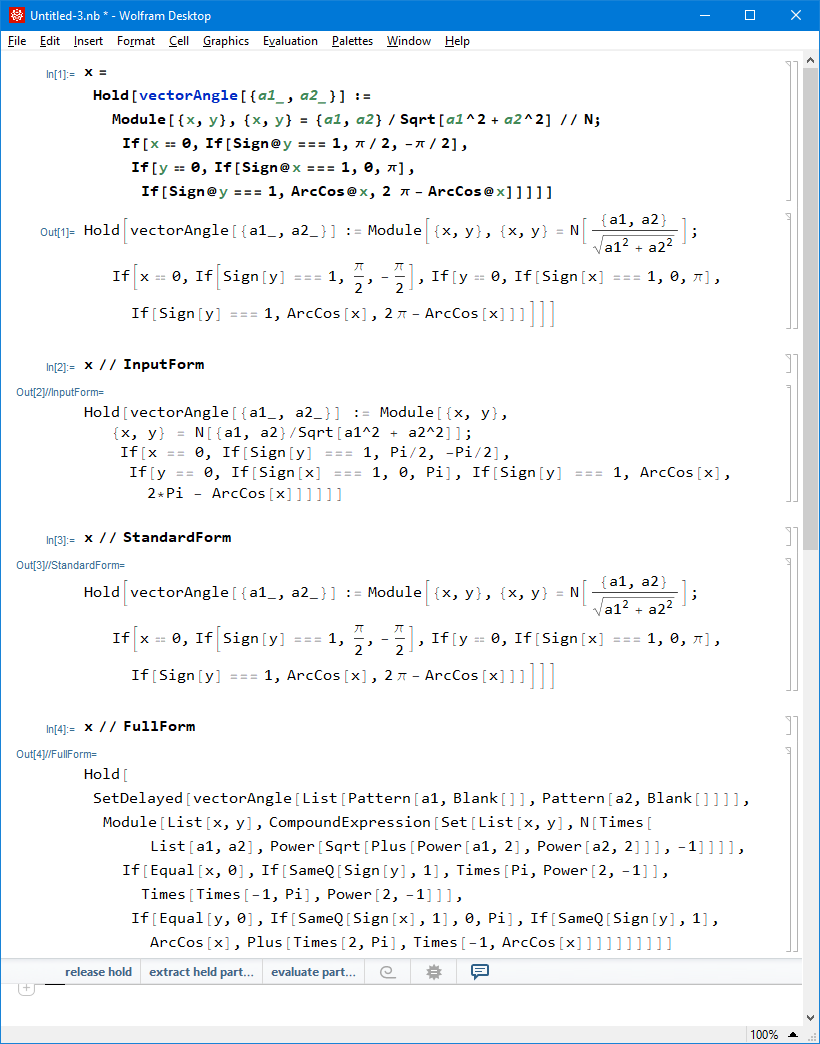
Here is a example of WolframLang syntax in FullForm.

SetDelayed[vectorAngle[List[Pattern[a1,Blank[]],Pattern[a2,Blank[]]]],
    Module[List[x,y],
      CompoundExpression[
        Set[List[x,y],
          N[Times[List[a1,a2],
              Power[Sqrt[Plus[Power[a1,2],Power[a2,2]]],-1]]]],
        If[Equal[x,0],
          If[SameQ[Sign[y],1],Times[Pi,Power[2,-1]],
            Times[Times[-1,Pi],Power[2,-1]]],
          If[Equal[y,0],If[SameQ[Sign[x],1],0,Pi],
            If[SameQ[Sign[y],1],ArcCos[x],
              Plus[Times[2,Pi],Times[-1,ArcCos[x]]]]]]]]]

Note the complete nested regularity F[…]. And the only character used are English alphabets, the square brackts, and comma. The whole language is just these character, corresponding to lisp's parenthesis and space.

Here is the same thing in lisp form. (called symbolic-expression (aka s-exp))

(SetDelayed
 (vectorAngle (list (Pattern a1 (Blank)) (Pattern a2 (Blank))))
 (let (list x y)
   (progn
    (setq (list x y)
          (N (* (list a1 a2)
                (exp (sqrt (+ (exp a1 2) (exp a2 2))) -1))))
    (if (eq x 0)
        (if (equal (signum y) 1) (* Pi (exp 2 -1))
          (* (* -1 Pi) (exp 2 -1)))
      (if (eq y 0) (if (equal (signum x) 1) 0 Pi)
        (if (equal (signum y) 1) (acos x)
          (+ (* 2 Pi) (* -1 (acos x)))))))))

Meta Expression

Following is the same thing in WolframLang InputForm. (which is a syntax layer on top of the regular nested form. Such is known as meta-expression (aka m-exp) in lisp world, conceived by lisp inventor John McCarthy, but never caught on in lisp comunity.)

vectorAngle[{a1_, a2_}] := Module[{x, y},
    {x, y} = {a1, a2}/Sqrt[a1^2 + a2^2] // N;
    If[x == 0, If[Sign@y === 1, Pi/2, -Pi/2],
      If[y == 0, If[Sign@x === 1, 0, Pi],
        If[Sign@y === 1, ArcCos@x, 2 Pi - ArcCos@x]]]]

Note the vectorAngle[{a1_, a2_}] := …? That's your lisp macros, but in a advanced form, called pattern matching. The “a1_” and “a2_” are patterns, and the right-hand-side is the transformation spec. 〔see Intro to Wolfram Language Pattern Matching for Lisp Programers〕

StandardForm (rendered display)

Following is the same thing rendered in WolframLang StandardForm.

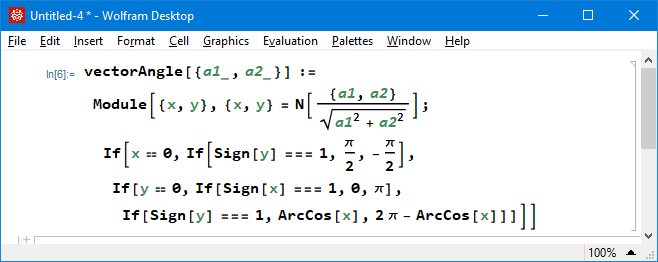
See also:

• Concepts and Confusions of Prefix, Infix, Postfix and Lisp Notations
• WolframLang: Syntax, Operators Cheatsheet