Programing Language Design: Why You Need Operators

Why Do We Need Operators in Programing Language, Why Not Just Function Calls

In scientific programing, you have to deal with math expressions often. Here is a quadratic formula in normal math notation:

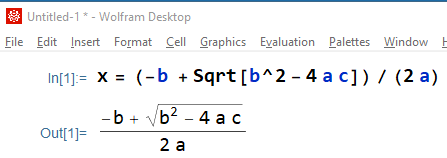
Here is functional notation in programing languages:

assign(x, div( plus(-b, sqrt( plus( power(b, 2), neg(times(4, a, c))))), times(2, a)))

If we allow symbols in function names, we have:

=(x, /( +(-b, √( +( ^(b, 2), -(*(4, a, c))))), *(2, a)))

in Lisp notation:

(set x (div (plus (neg b) (sqrt (power b 2) (neg (times 4 a c)))) (times 2 a )))

if we allow symbols, we have:

(= x (/ (+ (- b) (√ (^ b 2) (- (* 4 a c)))) (* 2 a )))

If we allow defining operators, we have the normal infix notation:

x = (-b + √(b^2 - 4 * a * c) ) / (2 * a)

If we allow space as implicit multiplication, we have the the shortest notation and most readable:

x = (-b + √(b^2 - 4 a c) ) / (2 a)

This is why operators in programing languages is essential for high-level programing languages in scientific programing.

Why Allow Users to Define Their Own Operators?

why is it good if a programing language allows you to define your own operators?

In programing, the datatypes are often arbitrarily defined by user, so you need to define your own operators such matrix multiplication and vector addition.

Real World Example in JavaScript

Here's real world example in JavaScript working with matrix and vectors.

Function notation with no math symbols

const svg_ellipse_arc = (([cx,cy],[rx,ry], [θ, Δ], φ ) => {
Δ = Δ % (2*π);
const rotMatrix = rotate_matrix (φ);
const [sX, sY] = vec_add ( matrix_times ( rotMatrix, [rx * cos(θ),ry * sin(θ)] ), [cx,cy] ) ;
const [eX, eY] = vec_add ( matrix_times ( rotMatrix, [rx * cos(θ+Δ),ry * sin(θ+Δ)] ), [cx,cy] ) ;
const fA = ( ( Math.abs (Δ) > π ) ? 1 : 0 );
const fS = ( ( Δ > 0 ) ? 1 : 0 );
const path = document.createElementNS("http://www.w3.org/2000/svg", "path");
path.setAttribute("d", "M " + sX + " " + sY + " A " + [ rx , ry , φ/π*180 , fA, fS, eX, eY ].join(" "));
return path;
});

Function notation with math symbols

Now, if we allow math symbols in names, we have:

const svg_ellipse_arc = (([cx,cy],[rx,ry], [θ, Δ], φ ) => {
Δ = Δ % (2*π);
const rotMatrix = rotate_matrix (φ);
const [sX, sY] = ⊕( ⊗( rotMatrix, [rx * cos(θ),ry * sin(θ)] ), [cx,cy] ) ;
const [eX, eY] = ⊕( ⊗( rotMatrix, [rx * cos(θ+Δ),ry * sin(θ+Δ)] ), [cx,cy] ) ;
const fA = ( ( Math.abs (Δ) > π ) ? 1 : 0 );
const fS = ( ( Δ > 0 ) ? 1 : 0 );
const path = document.createElementNS("http://www.w3.org/2000/svg", "path");
path.setAttribute("d", "M " + sX + " " + sY + " A " + [ rx , ry , φ/π*180 , fA, fS, eX, eY ].join(" "));
return path;
});

Operators with Math Symbols

Now, if we can define operators with math symbols in names, we have:

const svg_ellipse_arc = (([cx,cy],[rx,ry], [θ, Δ], φ ) => {
Δ = Δ % (2*π);
const rotMatrix = rotate_matrix (φ);
const [sX, sY] = rotMatrix ⊗ [rx * cos(θ),ry * sin(θ)] ⊕ [cx,cy];
const [sX, sY] = rotMatrix ⊗ [rx * cos(θ+Δ),ry * sin(θ+Δ)] ⊕ [cx,cy];
const fA = ( ( Math.abs (Δ) > π ) ? 1 : 0 );
const fS = ( ( Δ > 0 ) ? 1 : 0 );
const path = document.createElementNS("http://www.w3.org/2000/svg", "path");
path.setAttribute("d", "M " + sX + " " + sY + " A " + [ rx , ry , φ/π*180 , fA, fS, eX, eY ].join(" "));
return path;
});