Mathematical Simulation Ideas

Been thinking about writing some java applete in the past months. One particular is a go-game with different boards. (see my math games page about go.) As we know, go is played on a rectangular grid. However, we can think of a go variation on hexigonal grid or the triangular grid. On a rectangular grid, each point has 4 neighbors. On a hexigonal grid, 3 neighbors, and 6 neighbors for triangular grid. There are lots of regular tilings that can be used as go boards. This page explains it a bit: http://www.di.fc.ul.pt/~jpn/gv/boards.htm

I think studying these boards variations from a math point of view is rewarding, possibly contributing insight.

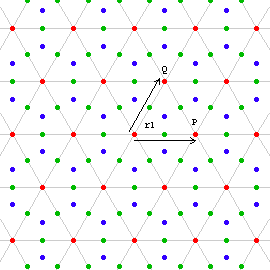
This image shows the triangular grid. A hexagonal grid is formed by the blue and green dots.

I've been using java in my previous job for about a year, but never really got the hang of it. In particular i want to study interface programing with its Swing module. I have never done interface programing before, so the prospects of writing a programing controlled by buttons and sliders and other widgets interactively is a novelty for me. Over the past decade, i had ideas about interactive math program that explore certain geometry aspects, but hasn't been realized partly because Mathematica cannot really create interactive programs. Here's some ideas i had in the past decade:

* Stereographic projection of a plane on a sphere. I want screen-saver like interactive program, that shows a plane represented by grids, with a sphere rolling freely on it, and the sphere is represented by grids that is a stereographic projection of the grid on the plane. Something like this. The idea is that i want to be able to visually see the image of the mapping. The grid on the plane can be animated for example, or start with any regular tilings.

The image of a grid of the function 1/Conjugate[x+y*I]

* interactive conic Sections . Conics sections is a rich subject. I want to write a interactive app that shows a cone and a plane, and their intersection. User can rotate the cone or plane by mouse drag. There should also be sliders and controllers for various parameters of the cone. And a pane should show their intersection in a plane, and also the corresponding equation. The gist, is a visual and instantaneous understanding of the various relations. There is a paradox i had, that a plane and a right cone couldn't form a ellipse, since ellipse is symmetric, while the cutting of a cone by a plane intuitively should form a egg shaped oval. Furthermore, a cylinder cut by a plane is also as ellipse. Thru a visual application, one could resolve this seeming paradox without words.

* relative motion. For example, the orbits of planets in the solar system. Relative to the sun, each planet moves in a elliptical path. But if we make one planet as the fixed point of reference, what would be the path of the other planets? When thinking about implementing this in a computer simulation, the answer rises. Basically, when one moving point is now fixed, the reference frame must now move in a motion of the fixed point. Thus, all objects's new motion would be the motion of the fixed object plus their own. Now, consider something like the moon orbiting the earth, while the earth moves around the sun, all in a plane. The sun is fixed, earth's path is a circle, while moon is some cycloid. If earth is the fixed reference, then sun's path is a circle around earth, and moon's paht is also a circle around earth. If moon is fixed, than earth moves around moon, and sun's path is some cycloid, which is a ciclular motion on top of another circular motion.

I've had this relative motion problem for years. Not until today actually thinking about implementing a program, the general solution comes. That is, when we want to fix on one moving object as the reference point, all the other's moving object's new motion is the motion of the fixed object plus their own. This solution adds some more thoughts. If we add a circular motion that is a small circle, and a elliptical motion that is very flat, there's the question of which one is base motion, because that can result different curves. If the circle is base, and we pick a direction of the ellipsoid, then we have a spirograph-like curve, itself is not a result of rolling two circles such as epitrochoid or hypotrochoid. On the other hand, if the long ellipsoid is the base curve, then we have stretched-spring-like drawings along a elliptical path. Also rises to the surface is that each motion is has a orientation. (for example, how the ellipse is oriented matters) Another thing to think about is what happens if we have two circles A and B, with A much bigger than B. What is the difference of the resulting curve when switch bases. A good interactive app with a slider can demonstrate this well. Showing the resulting additive curve, with a slider for size of A or B.

I'm much exposed to the idea of curves resulting from rolling one circle on another. I've also seen and read about curves that results as we add a rolling circle on another rolling circle. However, i've never thought of perhaps the more general idea of adding motions to another. Using ellipses as motions, i think this can at least explored as a decorative pattern a la spirographs.

After some experiment in Mathematica, this turned out to be not interesting. It essentially becomes adding two periodic curves by their parametric components. For example, if curve one is {t,t^2} and curve two {Sin[t],Cos[t]} and their “combined motion” would be {t+Sin[t],t^2+Cos[t]}. If both curves are periodic, then one gets some kind of screwy lissajou curve, not beautiful at all. Some thoughts previous thought is also wrong. Which one is “base curve” doesn't really matter, since such addition is communitive. The overall shape is not determined by their relative sizes, but relative period. Here's the mathematica notebook for play: additive_motions.nb