Hypotrochoid
Mathematica Notebook for This Page
History
See Epicycloid and Hypocycloid .
Description
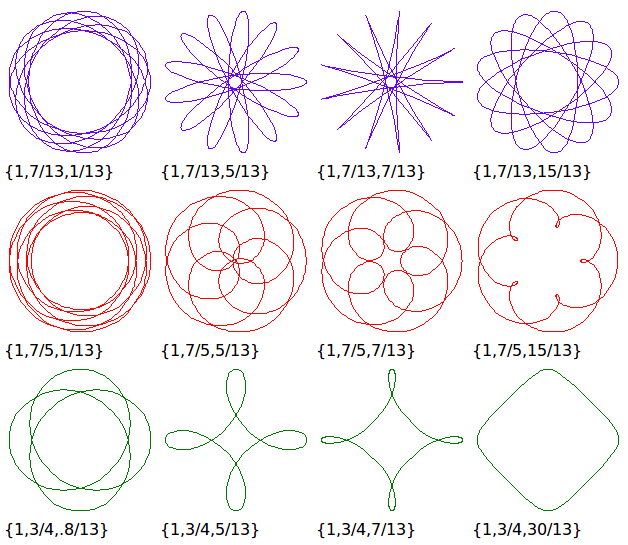
Hypotrochoid describes a family of curves. Hypotrochoid and epitrochoid are roulette of two circles. If one circle is inside another, the curve traced are called hypotrochoids. Otherwise (one rolls outside another), the curves are called epitrochoids. If the tracing point is on the (circumference) rolling circle, the curves are called hypocycloid or epicycloids. Hypotrochoids are also known as SpiroGraph, a tradmark of a toy that trace limited cases of hypotrochoids. Many famous curves are special cases of hypotrochoid. (See: Curve Family Index).
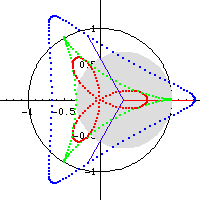
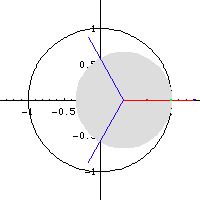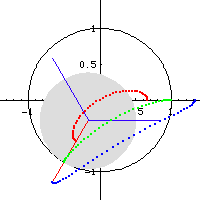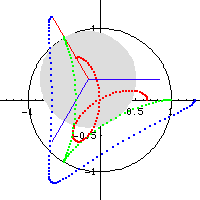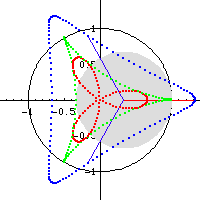
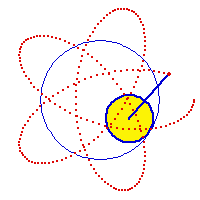
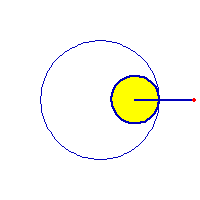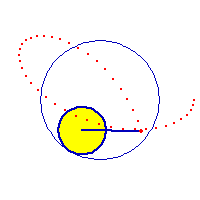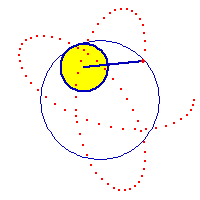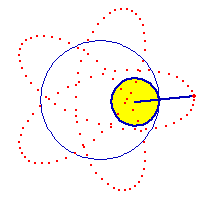
Formula
See Epicycloid and Hypocycloid .
Properties
Special Cases
h == 0, Circle.
b == h, hypocycloid with q cusps, where q is the denominator of b written as a irreducible fraction.
a/2 == b == h, Line of length 2 a.
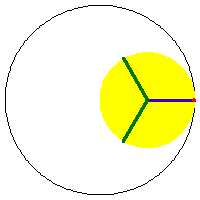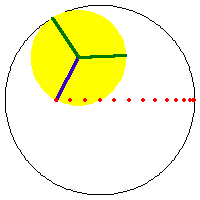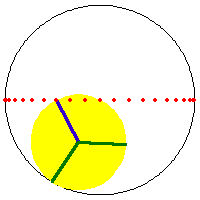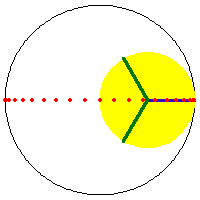
a/2 == b AND h ≠ b, ellipse with semimajor axis b+h and semiminor axis Abs[b-h].
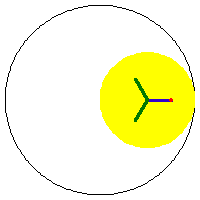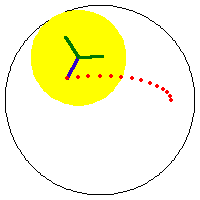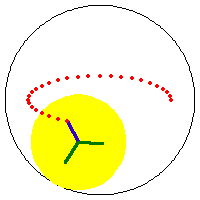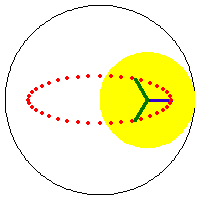
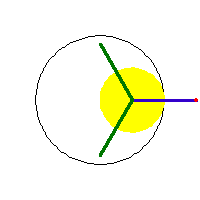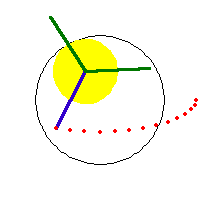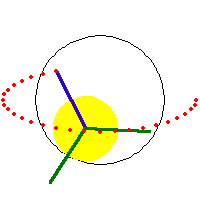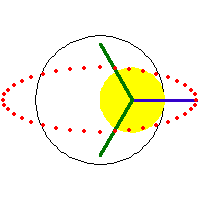
a/3 == b == h or 2/3 a == b == h, deltoid
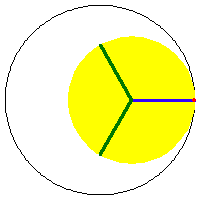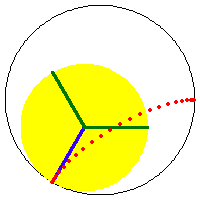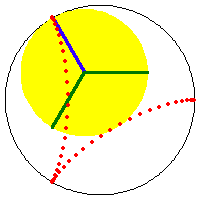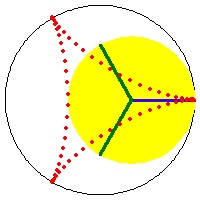
a/4 == b == h or 3/4 a == b == h, astroid
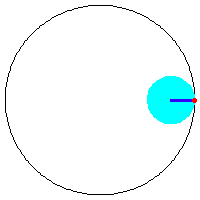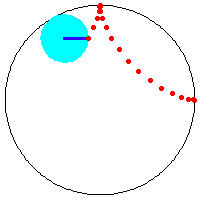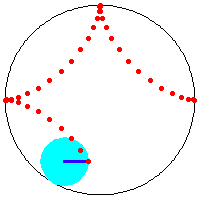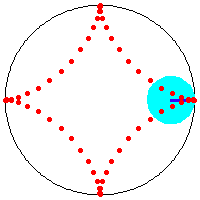
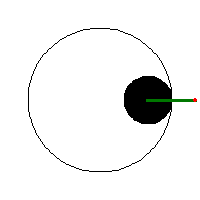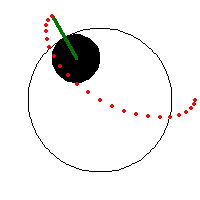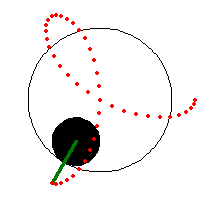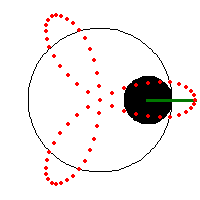
a = n/(n+1), b = (n-1)/(2 (n+1)), h = 1/2, n is a integer greater than 2, rose with n petals if n is odd, otherwise 2*n petals. One can multiply all parameters by (n+1)/n to get {1, (-1 + n)/(2 n), (1 + n)/(2 n)}. find the formula for double generation for rose
Mathematica spiral-graph generation template
Related Web Sites
See: Websites on Plane Curves, Plane Curves Books .
Robert Yates: Curves and Their Properties .