type theory
Reading Egbert Rijke Homotopy Type Theory Book vs Wikipedia
so much reading on type theory in past days.
The book Intro to Homotopy Type Theory by Egbert Rijke. I kinda abandoned reading it sequentially. It's not so good. I always go back to encyclopedia style materials instead. The text books, they usually try to teach by sequential manner, with each step detailed. But often, you end up stuck in one place on this linear road. Due to, i think often the author fails to be exacting in formal approach. (hard to do, cuz often you have to mention some concept before they are defined, and you also waddle in english, some parts have technical meaning to the topic, other parts are just english description of the topic, and sometimes you cannot tell which is which.)
Wikipedia and other online articles, allow you to freely jump, amass multiple views to get the concepts, even though each article may not be as professional or fully correct.
here's some random comments on the Wikipedia article Type theory first they described several types. e.g. empty type, unit type, boolean type, product type, sum type, natural numbers type.
but note, seems, some are a single type, while others are a class of types (many instances of such types). thus, they are meta descriptions of a set of types.
For empty type, unit type, boolean type, there seems to be just one type of each. But for product type, there are many such types. Same for sum type. But for the natural numbers type, again, just one such type.
In a sense, the product type is actually a class of types, or type of types. Thus, a meta description of types.
in other words, in a given formal type system, do you actually have a type, called “product type”, or is the phrase “product type” a description of a class of types in the type system? (i presume the latter.) If so, that means, there is no such thing as “product type”. The concept of “product type”, is just meta description for human to learn the type system. It does not exist. Is that right?
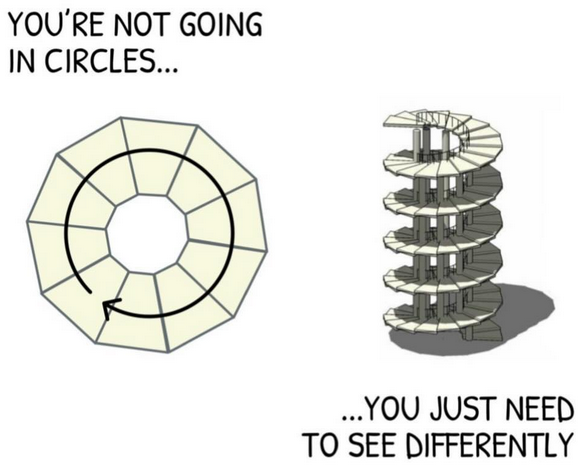
logic = tail chasing
this captures the evolution of logic / math foundation in past one hundred years. and that spiral, may not end.

lots reading on type theory in past days.
- Type theory
- https://plato.stanford.edu/entries/type-theory/
- https://ncatlab.org/nlab/show/type+theory
- https://plato.stanford.edu/entries/type-theory-church/
- this article, is written by
- Thierry Coquand, the guy who created coq and calculus of constructions.
- https://plato.stanford.edu/entries/type-theory/
Lambda Calculus 2013 By Henk Barendregt
Henk Barendregt home page https://www.cs.ru.nl/~henk/

- Lambda Calculus
- By Henk Barendregt.
- http://www.cs.ru.nl/~henk/Reflection/HL5.pdf
- (local copy HL5_tnzt.pdf)
- The Imperative and Functional Programming Paradigm
- By Henk Barendregta, Giulio Manzonettoa, Rinus Plasmeijer.
- http://www.cs.ru.nl/~henk/fp.pdf
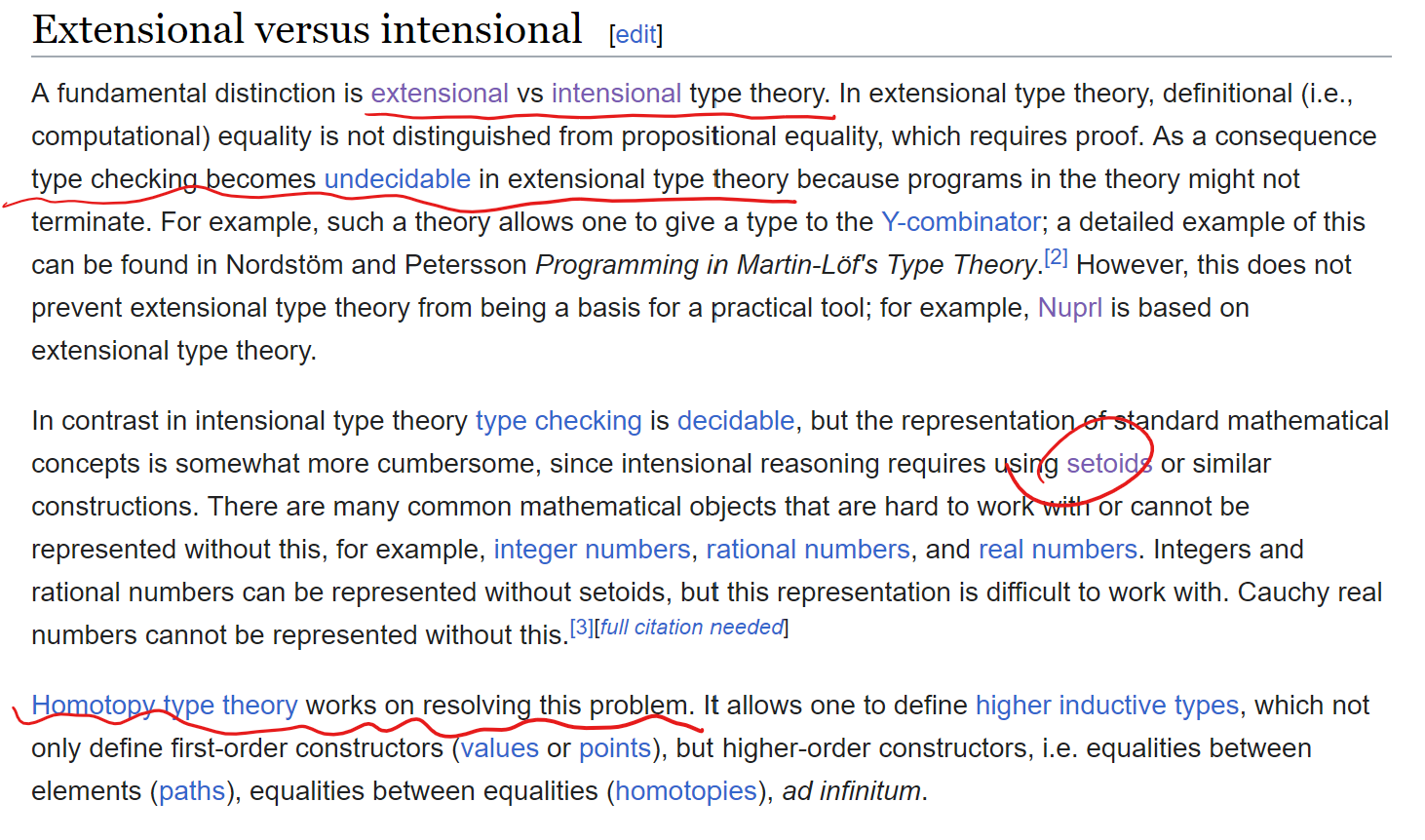
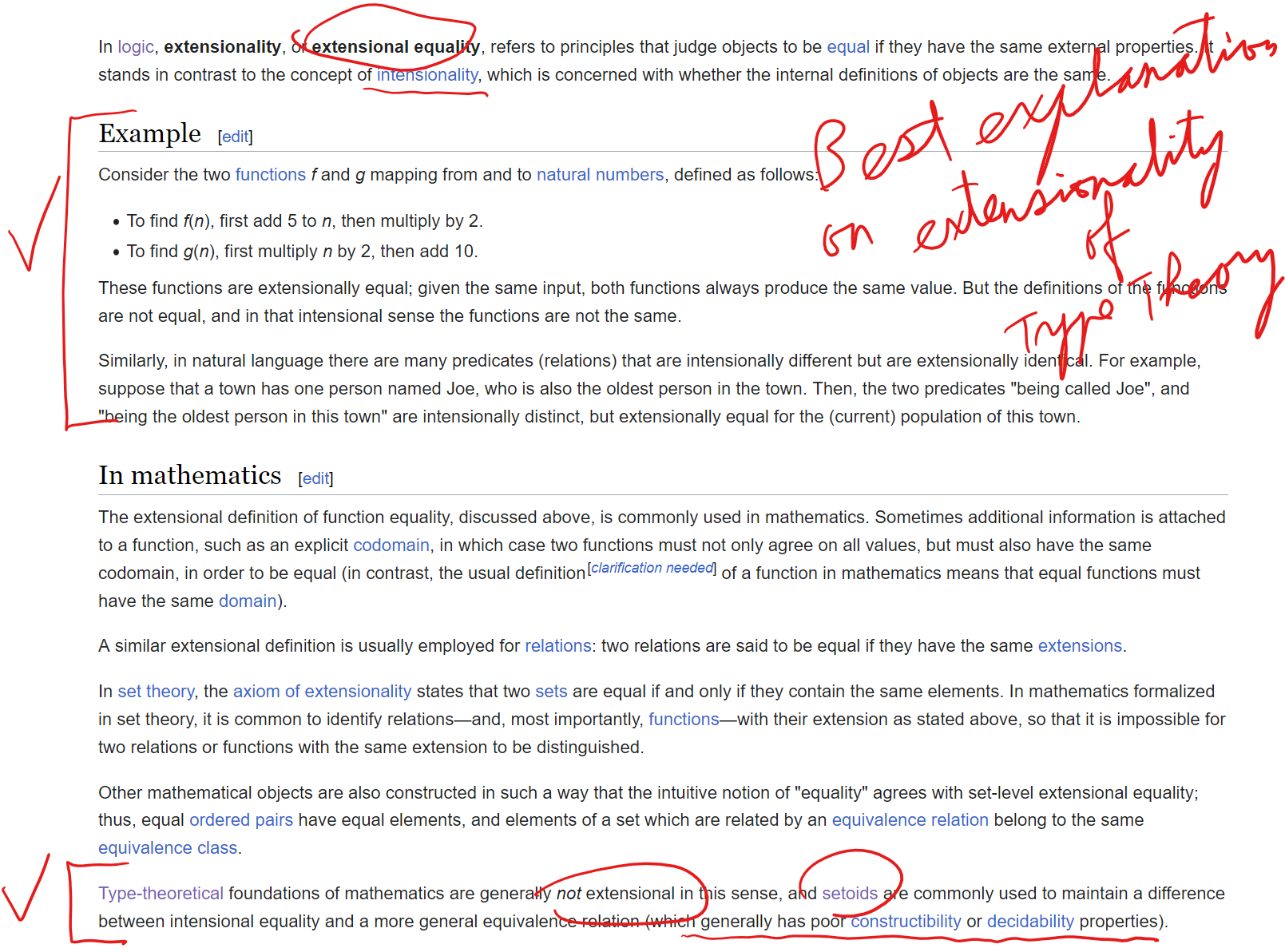
Type Theory, Extensional vs Intensional

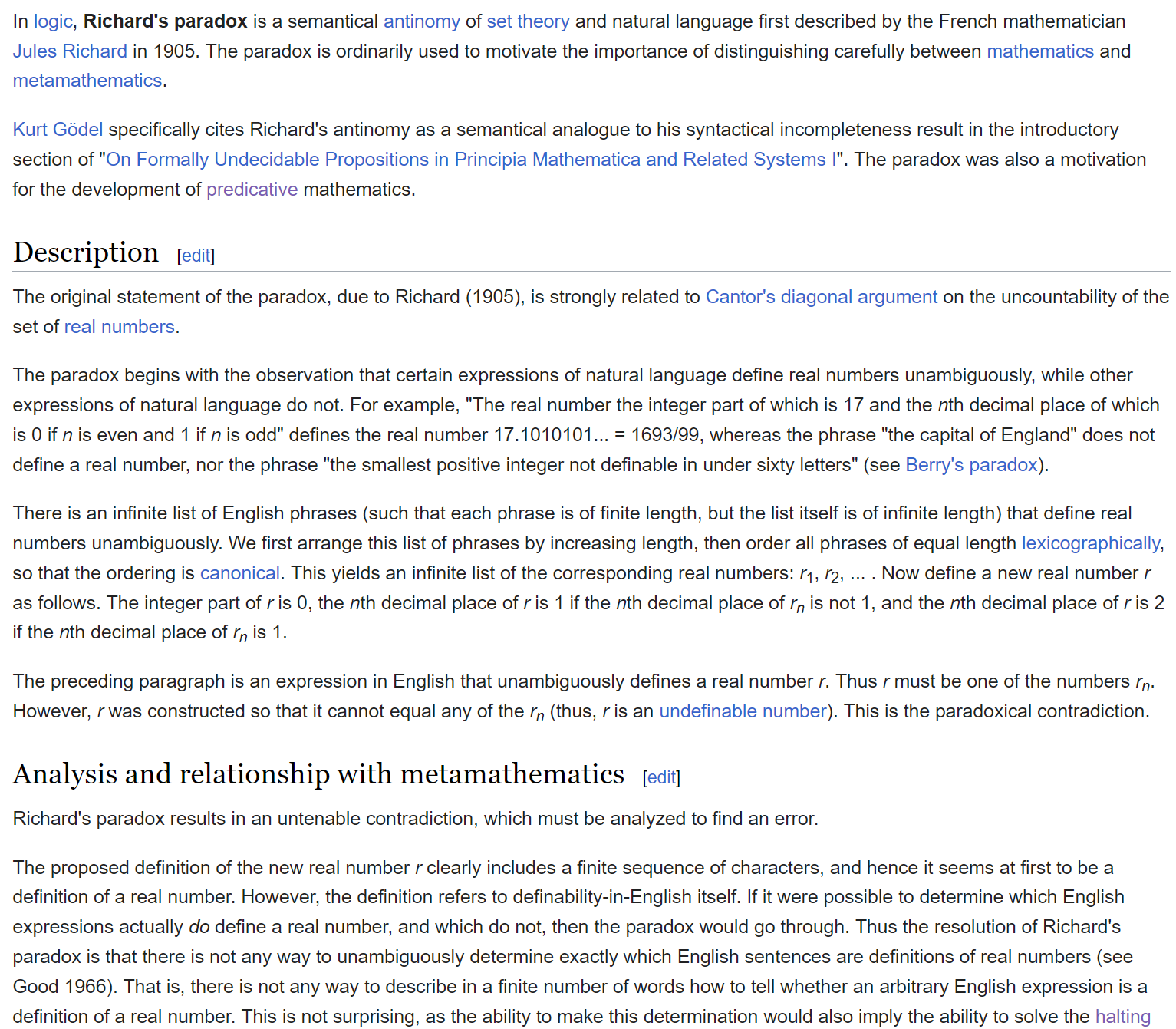
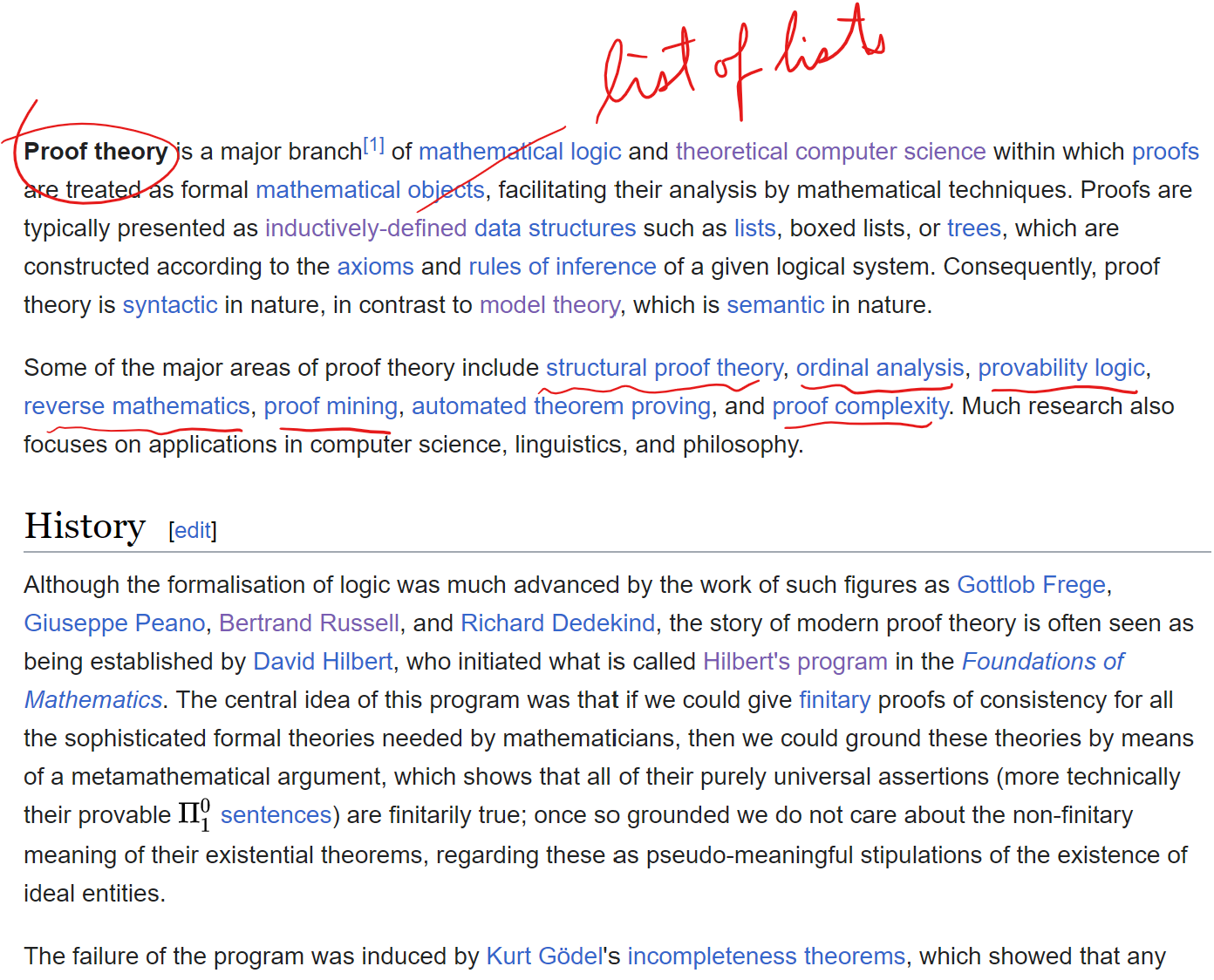
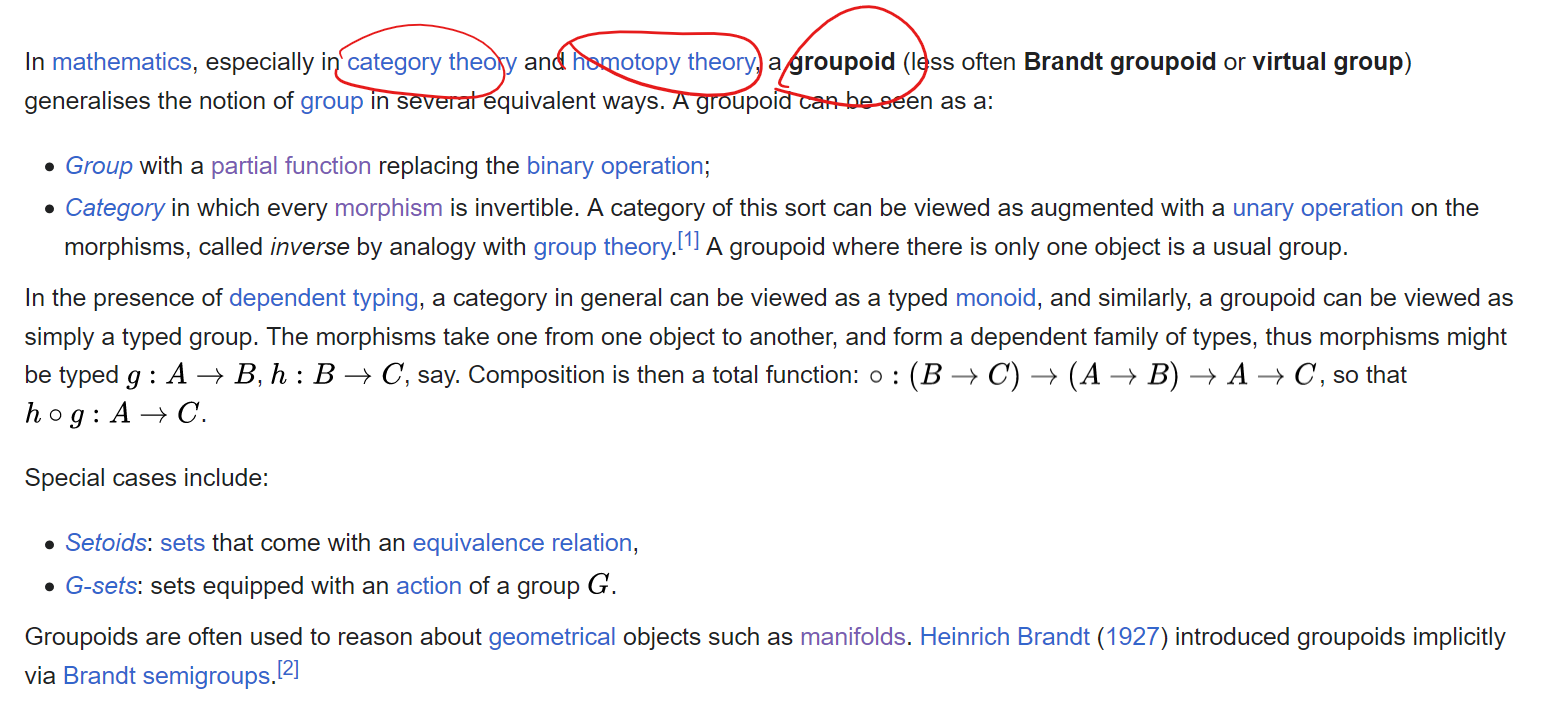
groupoid

new year resolution kinda todo
- what makes something turing equivalent, besides just modeling a turing machine or lambda calculus?
- need deep understanding of recursion theory. how it fits into the larger picture of logic and proof theories
- need to understand model theory. examples of it.
- need to have a survey understanding of logic.
- what is the different between propositional logic and syllogism.
- first order logic, and the higher orders. what are they, how they differ.
- understand the various logic, in particular, modal logic, non-standard logic, and their difference.
- need deep understanding of combinators and lambda calculus.
- need deep understanding of rewrite systems, ontology of it, and how they relate to lambda calculus. there is also string rewrite systems, tag system.
- in depth understanding the various type theory, lambda cube. sequent calculus.
- need deep understanding of models of computation
- Model of computation
- Sequential models
- Sequential models include:
- Finite state machines
- Post machines (Post–Turing machines and tag machines).
- Pushdown automata
- Register machines
- Random-access machines
- Turing machines
- Decision tree model
- Functional models
- Functional models include:
- Abstract rewriting systems
- Combinatory logic
- General recursive functions
- Lambda calculus
- Concurrent models
- Concurrent models include:
- Actor model
- Cellular automaton
- Interaction nets
- Kahn process networks
- Logic gates and digital circuits
- Petri nets
- Synchronous Data Flow
- Homotopy theory
- Type theory
- Intuitionistic type theory
- Setoid
- Intensional definition
- Intensional logic
- Univalence axiom
- Per Martin-Löf
- Proof assistant
- Higher-order logic
- History of type theory
- https://plato.stanford.edu/entries/type-theory/
- Impredicativity
- BHK interpretation
- Calculus of constructions
- Lambda cube
- https://lean-lang.org/functional_programming_in_lean/programs-proofs/tail-recursion.html
- the rules of type theory https://hott.github.io/HoTT-2019/images/mltt-rules.pdf
- Simply typed lambda calculus
- Richard's paradox
- Typed lambda calculus
- Pure type system
- Girard's paradox
- Structure (mathematical logic)#Many-sorted structures
- Proof theory
- Analytic proof
- Ordinal analysis
- Logic
- Natural deduction calculus
- First-order logic
- Fitch-style calculus#Example
- Sequent calculus