Xah Talk Show 2025-05-23 Ep660 Wolfram Language Animation

how to do animation in Wolfram language

• interactive animation.
• show sine, and in Manipulate, and ListAnimate
• show moving a circle, and animate it
• show Export, to mp4, and to gif

(* plot sine curve *)

Plot[Sin[x], {x,0,2 Pi}]

(* HHHH------------------------------ *)

(* generate a list of sine curve *)
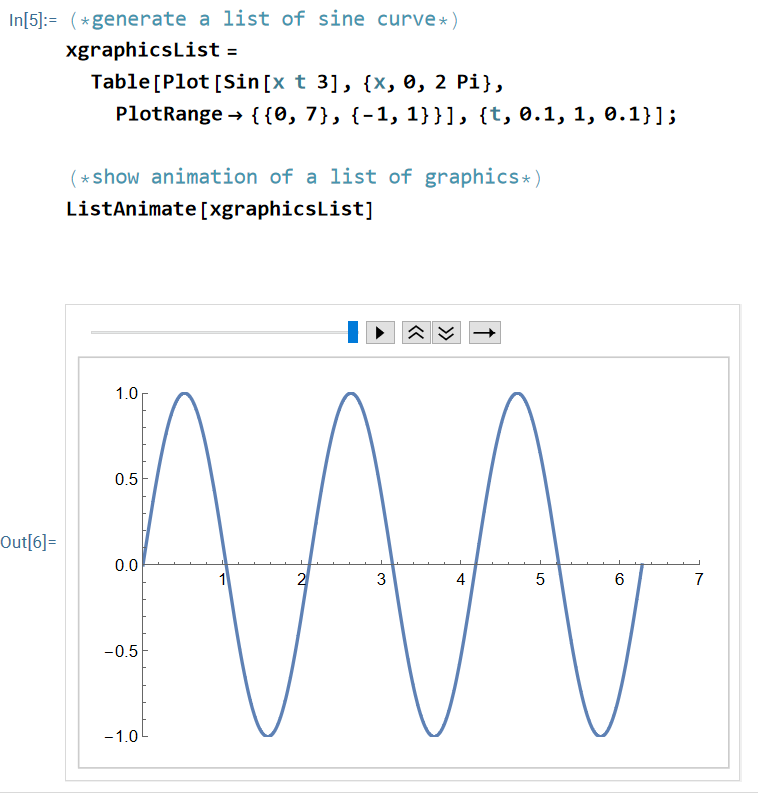
xgraphicsList=
Table[
Plot[Sin[x t], {x,0,2 Pi}, PlotRange -> {{0,7},{-1,1}}],
{t, 0.1, 1, 0.1}
];

(* show animation of a list of graphics *)
ListAnimate[ xgraphicsList ]

Export[ "sine_of_sine.mp4" , xgraphicsList]

(* HHHH------------------------------ *)

(* interactive graphics *)

Manipulate[
Plot[Sin[x t],{x,0,2 Pi},PlotRange->{{0,7},{-1,1}}],
{t, 0.1, 1, 0.1}
]

xx=
Manipulate[
 Plot[Sin[Sin[x]  t  2], {x, 0, 2  Pi},
  PlotRange -> {{0, 7}, {-1, 1}}], {t, 1, 2, 0.1}]

Export[ "sine_of_sine.mp4" , xx]

Export[ "sine_of_sine.gif" , xx]

(* HHHH------------------------------ *)

ListAnimate[
Table[
Plot[
x^3 - t  x^2
, {x,-5,5}, PlotRange -> {{0,7},{-1,1}}],
{t, 0.1, 1, 0.1}
]
]

create your own graphics for animation

(* move a circle *)

xgraphicsList =
 Table[Graphics[Circle[{t, 0}, 1], Axes -> True,
   PlotRange -> {{0, 10}, {-1, 1}}], {t, 0, 10, 1}]

(* show animation of a list of graphics *)
ListAnimate[ xgraphicsList ]

Export[ "moving circle.mp4" , xgraphicsList]

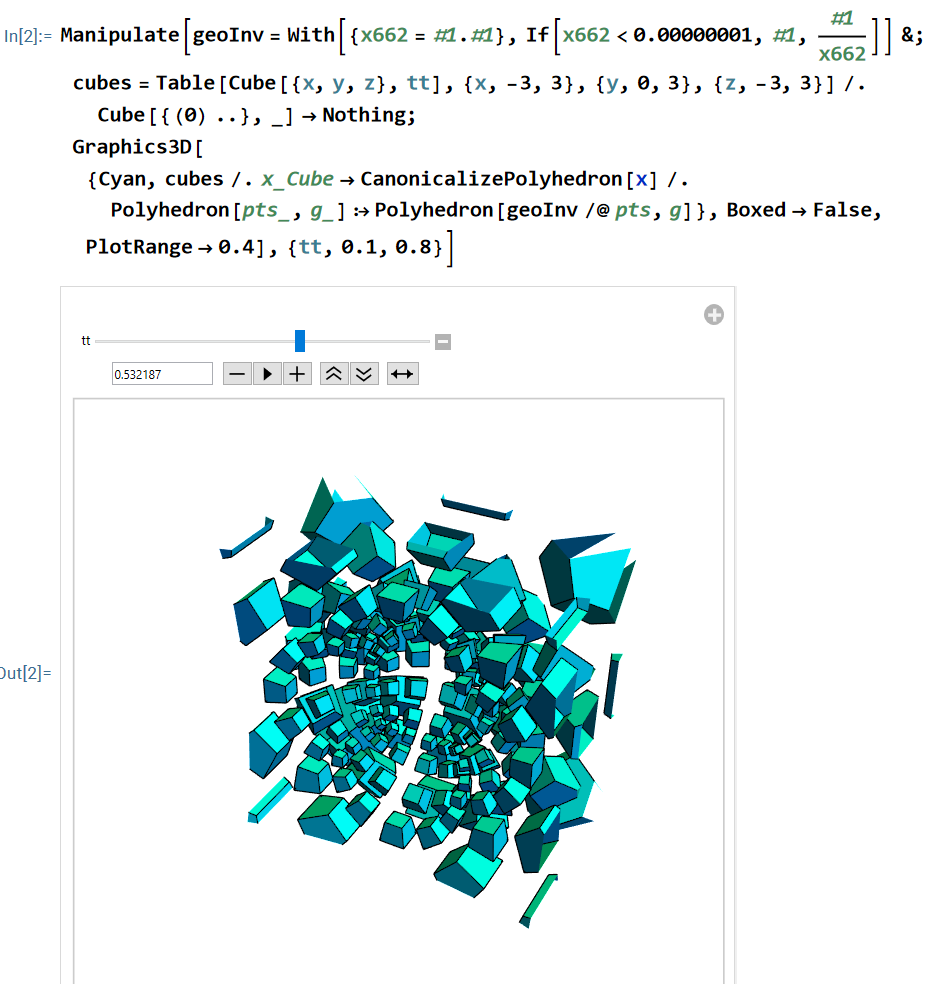
Example. 3d animation

• Fantastic geometric inversion of cubes.
• Animate tiny cubes to big.
• Wolfram language code.

• Xah Talk Show 2021-08-01 Math, Wolframlang Coding. Geometric Inversion of 3D Grid

Manipulate[
geoInv = ((With[{x662 = # . #},
      If[x662 < 0.00000001, #, #/x662]]) &);
cubes = Table[
    Cube[{x, y, z}, tt], {x, -3, 3}, {y, 0, 3}, {z, -3, 3}] /.
   Cube[{(0) ..}, _] -> Nothing;
Graphics3D[{Cyan,
  cubes /. x_Cube -> CanonicalizePolyhedron[x] /.
   Polyhedron[pts_, g_] :> Polyhedron[geoInv /@ pts, g]},
 Boxed -> False, PlotRange -> 0.4]
,
{tt, 0.1 , 0.8}
]