Epitrochoid and Hypotrochoid Animation Gallery

Snowflake1

(* snowflake.
 catacaustic of a hypotrochoid with varing parameter h *)

Needs["PlaneCurvePlot`"]
Needs["PlaneCurveFormulas`"]

xx = Table[
ParaPlot[
Evaluate @ Epitrochoid[1, 1/6, i][t],
{t, 0, 2 Pi, 2 Pi/(6 9)},
CausticLineLength->20,
Axes->False,PlotDot->False, PlotCurve->False,
CausticLineStyle->{Hue[0,0,1]},
Background->Hue[0,0,0],
PlotRange->{{-6,6},{-6,6}},
AspectRatio->Automatic
],
{i,0, 1.5, 1.5/40}
];

Snowflake 2

Snowflake
Based on catacaustic of a changing epitrochoid {1,1/6,h} with light source at the center.
The one on the right shows detail at the center.

(*
Snowflake2.
catacaustic of a hypotrochoid with varing parameter h
*)

Needs["PlaneCurvePlot`"]
Needs["PlaneCurveFormulas`"]

xx = Table[
ParaPlot[
Evaluate@Epitrochoid[1, 1/6, i][t], {t, 0, 2  Pi, 2  Pi/(6  9)},
CausticLineLength -> 20,
Axes -> False,
PlotDot -> False,
PlotCurve -> False, CausticLineStyle -> {Hue[0, 0, 1]},
Background -> Black,
PlotRange -> {{-2, 2}, {-2, 2}},
AspectRatio -> Automatic],
{i, 0, 1.5, 1.5/40}];

ListAnimate [xx, AnimationDirection -> ForwardBackward]

Atomic

spiralGraph — A hypotrochoid {1,6/13,h} with parameter h varing from .15 to 1.3. Each image is scaled so they all fit the display boundary.

Daze wheel

flashingIllusion — A illusion created by superimposing two hypotrochoids {1,1/7,2} rotating in opposite direction.

Flashing Diamond

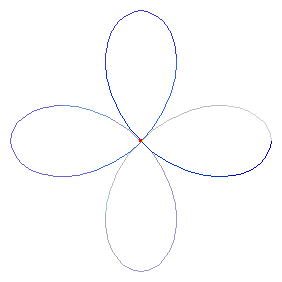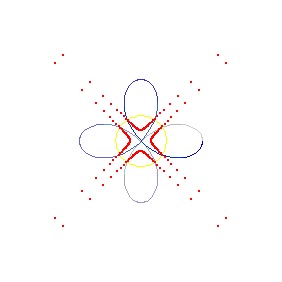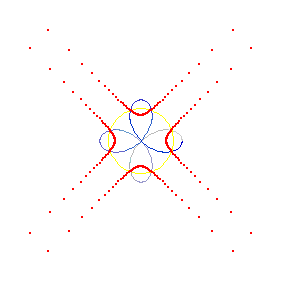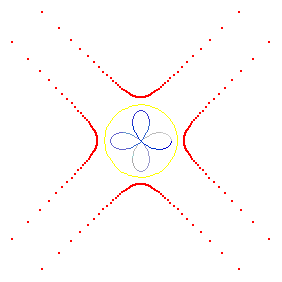
based on evolute of a hypotrochoid with varing parameter h. {1,1/4,h}

Flashing Diamond

(* Flashing Diamond. Evolute of a hypotrochoid with varing parameter h *)

Needs["PlaneCurvePlot`"]
Needs["PlaneCurveFormulas`"]

xx = Table[ParaPlot[
  Hypotrochoid[1, 1/4, i][t], {t, 0, 2  Pi, 2  Pi/(4  15)},
  PlotEvolute -> True, Axes -> False, PlotDot -> False,
  PlotCurve -> True,
  CurveColorFunction -> Blue, DotStyle -> {{Blue, PointSize[.01]}},
  LineStyle ->
   Red, AspectRatio -> Automatic,
  PlotRange -> {{-(1 - 1/4 + i), 1 - 1/4 + i}, {-(1 - 1/4 + i),
      1 - 1/4 + i}}  1.4], {i, 0, 1/4, (1/4)/100}]

ListAnimate [xx, AnimationDirection -> ForwardBackward]

Export["Flashing_Diamond_2025.mp4", xx ]

Supernova

based on evolute of ahypotrochoid with varing parameter h. {1,3/7,h}

(* SuperNova. Evolute of a hypotrochoid with varing parameter h *)

Needs["PlaneCurvePlot`"]
Needs["PlaneCurveFormulas`"]

Clear[xdotStyle,jj]

xdotStyle=Table[{PointSize[.01],Hue[i,3.33 (.3-i),1]},{i,0,.3,.3/39}];

xx =
Table[
 jj = (i 1/(3/7))^3;
 ParaPlot[
  Evaluate @
  Hypotrochoid[1, 3/7, jj][t],
  {t, 0, 18.22, 3 2 Pi/(7 40)},
  PlotEvolute->True,
  PlotCurve->False,
  DotStyle->xdotStyle,
  LineStyle->Yellow,
  Background -> Black,
  PlotRange->{{-1,1},{-1,1}} 1.05 (1+3/7+jj),
  AspectRatio->Automatic, Axes-> False
 ],
 {i, 0, .54, .54/30}
];

ListAnimate [xx, AnimationDirection -> ForwardBackward]

inverseRose — “Rose and Cotes' spiral”. Inverse of a quadrifolium {1, 1/4, 3/4} with respect to its center, and increasing radius of inversion. The resulting curve is a Cotes' spiral. (the red dots)

Kaleidoglass

Kaleidoglass 2025 xY82B

(* Kaleidoglass *)
(* Pedal of hypotrochoid with varing parameter h *)

Needs["PlaneCurvePlot`"]
Needs["PlaneCurveFormulas`"]

xx = Table[
 ParaPlot[
  Evaluate @ Hypotrochoid[1, 1/4, i][t],
  {t, 0, 2 Pi, 2 Pi/(4 21)},
  PedalPoint->{0,0},
  PlotDot->False,
  LineStyle->{Hue[.34,1,.8]},
  PlotRange->{{-(1-1/4+i),(1-1/4+i)},{-(1-1/4+i),(1-1/4+i)}} 1.05,
  Axes->False, AspectRatio->1
 ],{i,0/4,4/4, 1/100}
];

ListAnimate [xx, AnimationDirection -> ForwardBackward]

starfish

(* starfish *)
(* Secants of hypotrochoid with varing parameter h. *)

Needs["PlaneCurvePlot`"]
Needs["PlaneCurveFormulas`"]

xx = Table[j = (i  1/(2/5))^3;
  ParaPlot[
   Evaluate@Hypotrochoid[1, 2/5, j][t], {t, 0, 3  2  Pi,
    2  2  Pi/(5  22)}, SecantConnection -> {5  3, 1},
   CurveColorFunction -> Blue, Axes -> False, PlotDot -> False,
   AspectRatio -> Automatic,
   PlotRange -> {{-1, 1}, {-1, 1}}  (1 - 2/5 + j)  1.05], {i,
   0, .51, .51/60}]

ListAnimate [xx, AnimationDirection -> ForwardBackward]